Open Shading Language¶

Cycles Only

It is also possible to create your own nodes using Open Shading Language (OSL). Note that these nodes will only work for CPU rendering; there is no support for running OSL code on the GPU.

To enable it, select Open Shading Language as the shading system in the render settings.

Script Node¶

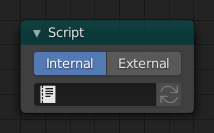
Script Node.¶

OSL was designed for node-based shading, and each OSL shader corresponds to one node in a node setup. To add an OSL shader, add a script node and link it to a text data-block or an external file. Input and output sockets will be created from the shader parameters on clicking the update button in the Node or the Text editor.

OSL shaders can be linked to the node in a few different ways. With the Internal mode, a text data-block is used to store the OSL shader, and the OSO bytecode is stored in the node itself. This is useful for distributing a blend-file with everything packed into it.

The External mode can be used to specify a .osl file from a drive, and this will then be automatically compiled into a .oso file in the same directory. It is also possible to specify a path to a .oso file, which will then be used directly, with compilation done manually by the user. The third option is to specify just the module name, which will be looked up in the shader search path.

The shader search path is located in the same place as the scripts or configuration path, under:

Linux

$HOME/.config/blender/2.92/shaders/

Windows

C:\Users\$user\AppData\Roaming\Blender Foundation\Blender\2.92\shaders\

macOS

/Users/$USER/Library/Application Support/Blender/2.92/shaders/

Tip

For use in production, we suggest to use a node group to wrap shader script nodes, and link that into other blend-files. This makes it easier to make changes to the node afterwards as sockets are added or removed, without having to update the script nodes in all files.

Writing Shaders¶

For more details on how to write shaders, see the OSL specification. Here is a simple example:

shader simple_material(
    color Diffuse_Color = color(0.6, 0.8, 0.6),
    float Noise_Factor = 0.5,
    output closure color BSDF = diffuse(N))
{
    color material_color = Diffuse_Color * mix(1.0, noise(P * 10.0), Noise_Factor);
    BSDF = material_color * diffuse(N);
}

Closures¶

OSL is different from, for example, RSL or GLSL, in that it does not have a light loop. There is no access to lights in the scene, and the material must be built from closures that are implemented in the renderer itself. This is more limited, but also makes it possible for the renderer to do optimizations and ensure all shaders can be importance sampled.

The available closures in Cycles correspond to the shader nodes and their sockets; for more details on what they do and the meaning of the parameters, see the shader nodes manual.

BSDF¶

diffuse(N)
oren_nayar(N, roughness)
diffuse_ramp(N, colors[8])
phong_ramp(N, exponent, colors[8])
diffuse_toon(N, size, smooth)
glossy_toon(N, size, smooth)
translucent(N)
reflection(N)
refraction(N, ior)
transparent()
microfacet_ggx(N, roughness)
microfacet_ggx_aniso(N, T, ax, ay)
microfacet_ggx_refraction(N, roughness, ior)
microfacet_beckmann(N, roughness)
microfacet_beckmann_aniso(N, T, ax, ay)
microfacet_beckmann_refraction(N, roughness, ior)
ashikhmin_shirley(N, T, ax, ay)
ashikhmin_velvet(N, roughness)

Hair¶

hair_reflection(N, roughnessu, roughnessv, T, offset)
hair_transmission(N, roughnessu, roughnessv, T, offset)
principled_hair(N, absorption, roughness, radial_roughness, coat, offset, IOR)

BSSRDF¶

bssrdf_cubic(N, radius, texture_blur, sharpness)
bssrdf_gaussian(N, radius, texture_blur)

Volume¶

henyey_greenstein(g)
absorption()

Other¶

emission()
ambient_occlusion()
holdout()
background()

Attributes¶

Some object, particle and mesh attributes are available to the built-in getattribute() function. UV maps and vertex colors can be retrieved using their name. Other attributes are listed below:

geom:generated: Generated texture coordinates.
geom:uv: Default render UV map.
geom:dupli_generated: For instances, generated coordinate from duplicator object.
geom:dupli_uv: For instances, UV coordinate from duplicator object.
geom:trianglevertices: 3 vertex coordinates of the triangle.
geom:numpolyvertices: Number of vertices in the polygon (always returns three currently).
geom:polyvertices: Vertex coordinates array of the polygon (always three vertices currently).
geom:name: Name of the object.
geom:is_curve: Is object a strand or not.
geom:curve_intercept: Point along the strand, from root to tip.
geom:curve_thickness: Thickness of the strand.
geom:curve_tangent_normal: Tangent Normal of the strand.
path:ray_length: Ray distance since last hit.
object:location: Object location.
object:index: Object index number.
object:random: Per object random number generated from object index and name.
material:index: Material index number.
particle:index: Particle instance number.
particle:age: Particle age in frames.
particle:lifetime: Total lifespan of particle in frames.
particle:location: Location of the particle.
particle:size: Size of the particle.
particle:velocity: Velocity of the particle.
particle:angular_velocity: Angular velocity of the particle.

Trace¶

We support the trace(point pos, vector dir, ...) function, to trace rays from the OSL shader. The “shade” parameter is not supported currently, but attributes can be retrieved from the object that was hit using the getmessage("trace", ..) function. See the OSL specification for details on how to use this.

This function cannot be used instead of lighting; the main purpose is to allow shaders to “probe” nearby geometry, for example to apply a projected texture that can be blocked by geometry, apply more “wear” to exposed geometry, or make other ambient occlusion-like effects.

Join the 2%