Structure¶
Example of a very basic armature.¶
Armatures mimic real skeletons. They are made out of bones, which are (by default) rigid elements. But you have more possibilities than with real skeletons: In addition to the "natural" rotation of bones, you can also move and even scale them! And your bones do not have to be connected to each other; they can be completely free if you want. However, the most natural and useful setups imply that some bones are related to others, forming so-called "chains of bones", which create some sort of "limbs" in your armature, as detailed in Chains of Bones.
Chains of Bones¶
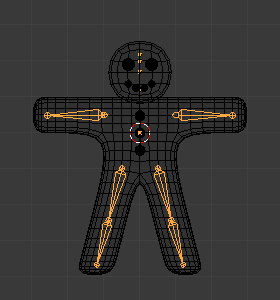
The bones inside an armature can be completely independent from each other (i.e. the modification of one bone does not affect the others). But this is not often a useful set up: To create a leg, all bones "after" the thigh bone should move "with" it in a well-coordinated manner. This is exactly what happens in armatures by parenting a bone to the next one in the limb, you create a "chains of bones". These chains can be ramified. For example, five fingers attached to a single "hand" bone.

An armature with two chains of bones.¶
Bones are chained by linking the tip of the parent to the root of the child. Root and tip can be connected, i.e. they are always exactly at the same point; or they can be free, like in a standard parent-child object relationship.
A given bone can be the parent of several children, and hence be part of several chains at the same time.
The bone at the beginning of a chain is called its root bone, and the last bone of a chain is the tip bone (do not confuse them with similar names of bones' joints!).
Chains of bones are a particularly important topic in posing (especially with the standard forward kinematics versus "automatic" inverse kinematics posing techniques). You create/edit them in Edit Mode, but except in case of connected bones, their relationships have no effect on bone transformations in this mode (i.e. transforming a parent bone will not affect its children).
The easiest way to manage bones relationships is to use the Relations panel in the Bone tab.