Select Loops

Select Edge Loops

Reference

Mode

Edit Mode (Vertex or Edge select mode)

選單

Select ‣ Select Loops ‣ Edge Loops

Shortcut

Alt-LMB, or Shift-Alt-LMB for modifying existing selection.

Holding Alt while selecting an edge selects a loop of edges that are connected in a line end-to-end, passing through the edge under the mouse pointer. Holding Shift-Alt while clicking adds to the current selection.

Note

Vertex mode

In Vertex select mode, you can also select edge loops, by using the same shortcuts, and clicking on the edges (not on the vertices).

Longitudinal and latitudinal edge loops.

The left sphere shows an edge that was selected longitudinally. Notice how the loop is open. This is because the algorithm hit the vertices at the poles and is terminated because the vertices at the pole connect to more than four edges. However, the right sphere shows an edge that was selected latitudinally and has formed a closed loop. This is because the algorithm hit the first edge that it started with.

Select Edge Loops (All Boundaries)

All boundary edges can be selected by performing a second loop select action on a boundary edge.

This can be useful for selecting boundaries for meshes that include triangles and n-gons, where loop select would not otherwise select the full boundary.

The second loop select action is shown on the right.

Select Face Loops

Reference

Mode

Edit Mode (Face or Vertex select modes)

Shortcut

Alt-LMB or Shift-Alt-LMB for modifying existing selection.

In face select mode, holding Alt while selecting an edge selects a loop of faces that are connected in a line end-to-end, along their opposite edges.

In vertex select mode, the same can be accomplished by using Ctrl-Alt to select an edge, which selects the face loop implicitly.

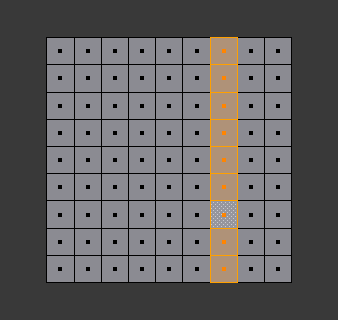
Face loop selection.

This face loop was selected by clicking with Alt-LMB on an edge, in face select mode. The loop extends perpendicular from the edge that was selected.

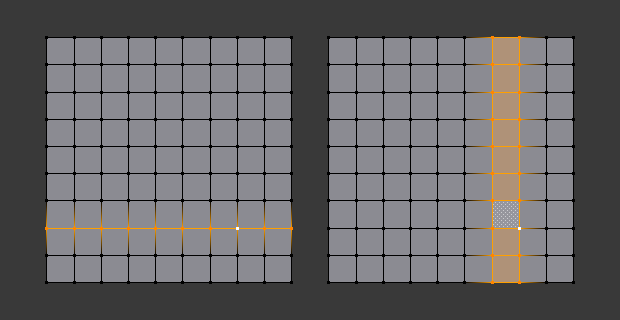
Alt versus Ctrl-Alt in vertex select mode.

A face loop can also be selected in Vertex select mode. Technically Ctrl-Alt-LMB will select an Edge Ring, however, in Vertex select mode, selecting an Edge Ring implicitly selects a Face Loop since selecting opposite edges of a face implicitly selects the entire face.

Select Edge Rings

Reference

Mode

編輯模式

選單

Select ‣ Select Loops ‣ Edge Rings

Shortcut

Ctrl-Alt-LMB

In Edge select mode, holding Ctrl-Alt while selecting an edge (or two vertices) selects a sequence of edges that are not connected, but on opposite sides to each other continuing along a face loop.

As with edge loops, you can also select edge rings based on current selection, using either Select ‣ Select Loops ‣ Edge Rings.

Note

Vertex mode

In Vertex select mode, you can use the same shortcuts when clicking on the edges (not on the vertices), but this will directly select the corresponding face loop...

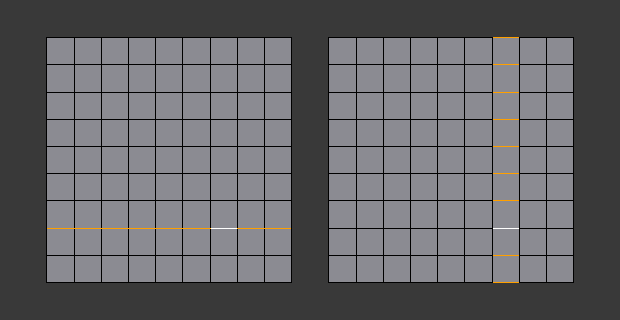
A selected edge loop, and a selected edge ring.

In Fig. A selected edge loop, and a selected edge ring. the same edge was clicked on, but two different "groups of edges" were selected, based on the different tools. One is based on edges during computation and the other is based on faces.

Note

Convert Selection to Whole Faces

If the edge ring selection happened in Edge Select Mode, switching to Face Select Mode will erase the selection.

This is because none of those faces had all its (four) edges selected, just two of them.

Instead of selecting the missing edges manually or by using Shift-Alt-LMB twice, it is easier to first switch to Vertex Select Mode, which will kind of "flood" the selection. A subsequent switch to Face Select Mode will then properly select the faces.

Select Loop Inner-Region

Reference

Mode

Edit Mode (Edge select mode)

選單

Select ‣ Select Loops ‣ Select Loop Inner-Region

Select Loop Inner-Region selects all faces that are inside a closed loop of edges. While it is possible to use this operator in Vertex and Face selection modes, results may be unexpected. Note that if the selected loop of edges is not closed, then all connected edges on the mesh will be considered inside the loop.

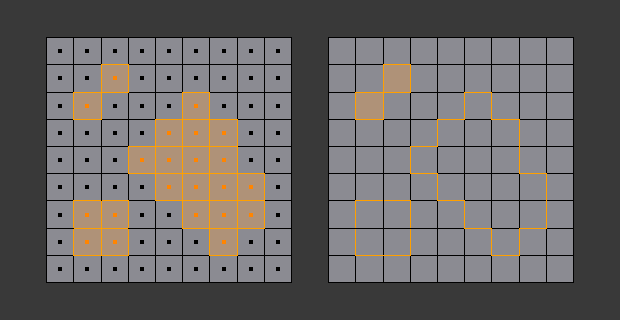
Loop to Region.

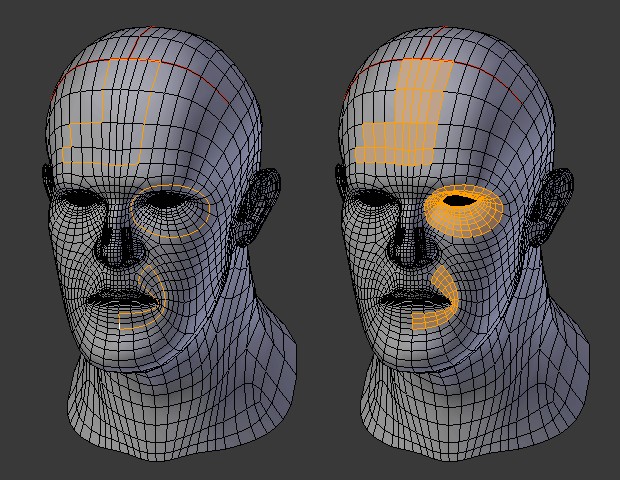
This tool handles multiple loops fine, as you can see.

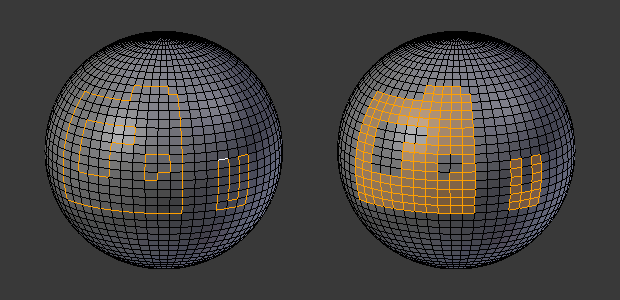
This tool handles "holes" just fine as well.

Select Boundary Loop

Reference

Mode

Edit Mode (Edge select mode)

選單

Select ‣ Select Loops ‣ Select Boundary Loop

Select Boundary Loop does the opposite of Select Loop Inner-Region, based on all regions currently selected, it selects only the edges at the border (contour) of these islands. It can operate in any select mode, but when in Face mode it will switch to Edge select mode after running.

All this is much more simple to illustrate with examples:

Select Boundary Loop does the opposite and forces into Edge Select Mode.