Estructura
Splines
Las splines son una subestructura de las curvas y son los elementos individuales que forman los objetos de curva. Un objeto de curva puede estar compuesto por varias splines diferentes, al igual que los objetos de malla pueden tener diferentes mallas discontinuas debajo del mismo objeto. Una spline define la forma de la curva y se puede transformar modificando sus Puntos de Control. Las splines vienen en tres tipos distintos, que se describen en Tipos de Spline. Cada tipo de spline tiene un algoritmo ligeramente diferente para calcular cómo se representan las curvas en la spline.
Las splines tienen sus propias propiedades independientes de las curvas y se pueden modificar seleccionando la spline en el Modo Edición y utilizando el panel Curva Activa.
Puntos de control
Al igual que las mallas, las splines tienen puntos de control o vértices. Los puntos de control se conectan a otros puntos de control para formar splines. Los puntos de control pueden ser seleccionados y transformados para alterar la forma resultante de la spline.
Ver también
Tipos de curvas
Polígono
Las spline poligonales son el tipo de spline más simple, ya que no interpolan la forma de la curva entre los puntos de control.
Las curvas poligonales se utilizan al convertir mallas en curvas. Debido a que no interpolan la forma, las curvas poligonales podrán brindar una representación precisa de la malla original del objeto.
Este es el caso de uso principal de las curvas, la mayoría de las veces se utilizarán curvas Bezier o NURBS en su lugar; ambos tipos interpolarán la forma y producirán resultados suaves.
Bezier
Los principales elementos utilizados en la edición de curvas Bezier son los puntos de control y las asas. Un segmento (de curva) se encontrará entre dos puntos de control. Las asas definirán la curvatura del segmento.
En la imagen a continuación, los puntos de control se pueden encontrar en el medio de la línea rosa, mientras que las asas comprenden las extensiones desde el punto de control. Las flechas visualizan las normales de la curva, que indican, por ejemplo, la dirección y la inclinación.
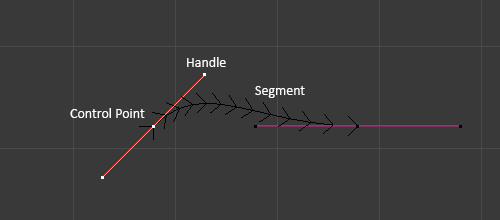
Curva Bezier en modo Edición.
Tipos de Asa
Existen cuatro tipos de asas de curva Bezier. Será posible acceder a ellas presionando V y seleccionando de la lista emergente.

Tipos de asas de curvas Bezier.
- Automático (asas amarillas)
Este asa tiene una longitud y una dirección completamente automáticas que Blender establece para garantizar el resultado más suave. Estas asas se convierten en asas Alineadas cuando se mueven.
- Vector (asas verdes)
Ambas partes de un asa siempre apuntan al asa anterior o al asa siguiente, lo que le permite crear curvas o secciones de las mismas hechas de líneas rectas o con esquinas definidas. Las asas vectoriales se convierten en asas Libres cuando se mueven.
- Alineada (asas moradas)
Estas asas siempre se encuentran en línea recta y dan una curva continua sin ángulos agudos.
- Libre (asas negras)
Las asas son independientes entre sí.
NURBS
N.U.R.B.S. es la abreviatura de «spline básica racional no uniforme» (en inglés: Non-uniform Rational Basis Spline). Una de las principales diferencias entre Bezier y NURBS es que las curvas Bezier son aproximaciones. Por ejemplo, un círculo Bezier es una aproximación a un círculo, mientras que un círculo NURBS es un círculo exacto. La teoría NURBS puede ser un tema muy complicado. Para una introducción, consultar la página de Wikipedia.
Los puntos de control de spline NURBS son diferentes a otros tipos de spline porque tienen una propiedad de influencia especial. Esta propiedad de influencia controla cuánta influencia tiene el punto de control en la superficie. Esta influencia no debe confundirse con la Influencia Ideal, que se usa sólo para simulaciones de cuerpos blandos. La influencia del punto de control NURBS se puede ajustar en el campo numérico W del panel de Transformación.
Nota
Si todos los puntos de control tienen la misma Influencia, entonces cada uno se cancela entre sí. Es la diferencia en las influencias lo que hace que la curva se acerque o se aleje de un punto de control.