Uvod
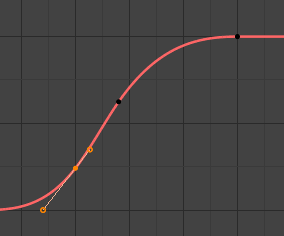
After animating some property in Blender using keyframes you can edit their corresponding curves. When something is „animated“, it changes over time. This curve is shown as something called an F-Curve. Basically what an F-Curve does is an interpolation between two animated properties. In Blender, animating an object means changing one of its properties, such as the object’s location, or its scale.
As mentioned, Blender’s fundamental unit of time is the „frame“, which usually lasts just a fraction of a second, depending on the frame rate of the scene. As animation is composed of incremental changes spanning multiple frames, usually these properties are not manually modified frame-by-frame, because:
It would take ages!
It would be very difficult to get smooth variations of the property (unless you compute mathematical functions and type a precise value for each frame, which would be crazy).
This is why nearly all direct animation is done using interpolation.
The idea is simple: you define a few Keyframes, which are multiple frames apart. Between these keyframes, the properties‘ values are computed (interpolated) by Blender and filled in. Thus, the animators‘ workload is significantly reduced.
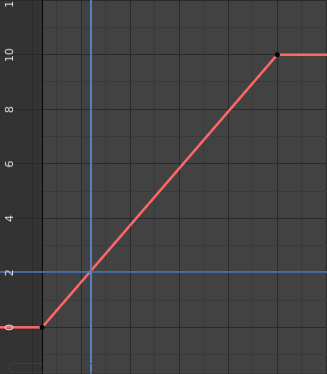
Example of an interpolation.
For example, if you have:
A control point of value 0 at frame 0,
another one of value 10 at frame 25,
and you use linear interpolation, then, at frame 5 we get a value of 2.
The same goes for all intermediate frames: with just two points, you get a smooth increase from (0 to 10) along the 25 frames. Obviously, if you would like the frame 15 to have a value of 9, you would have to add another control point (or keyframe)…
Direction of Time
Although F-Curves are very similar to Bézier, there are some important differences.
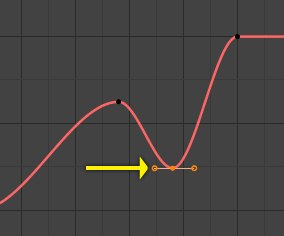
For obvious reasons, a property represented by a curve cannot have more than one value at a given time, hence:
When you move a control point ahead of a control point that was previously ahead of the point that you are moving, the two control points switch their order in the edited curve, to avoid the curve going back in time.
For the above reason, it is impossible to have a closed F-Curve.
Before moving the second keyframe. |
After moving the second keyframe. |