拉普拉斯形变修改器¶
拉普拉斯形变 修改器允许你在为网格摆姿势的同时,保留表面的几何体的细节。
用户定义一组 锚点 顶点,然后移动其中一些顶点。 修改器将其余锚点顶点保持在固定位置,并计算所有剩余顶点的最佳位置以保留原始几何细节。
该修改器采用微分坐标来捕获几何细节。微分坐标根据相邻的顶点来捕获当前顶点的曲率、方向等局部几何信息。
Note
必须定义 锚点顶点组 ,否则修改器不作任何操作。
选项¶
拉普拉斯形变修改器.¶
- 重复
进行多少次迭代来改进找到的解决方案。其目的是找出保持最佳几何细节的微分坐标的旋转。如果使用更多的迭代,细节会被更好地保留,但是计算会花费更长的时间。
Deform horse example blend-file.¶ 
原始模型。¶
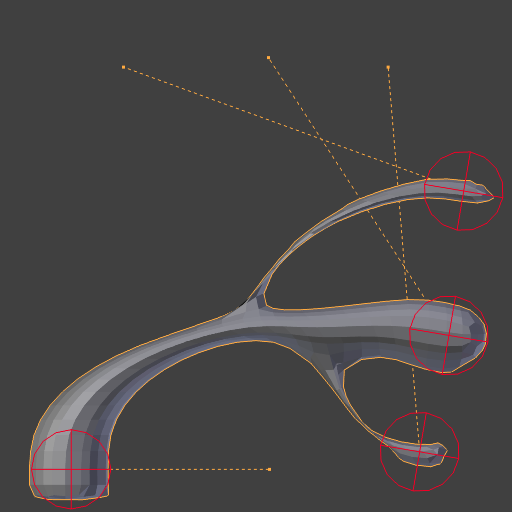
重复: 1.¶
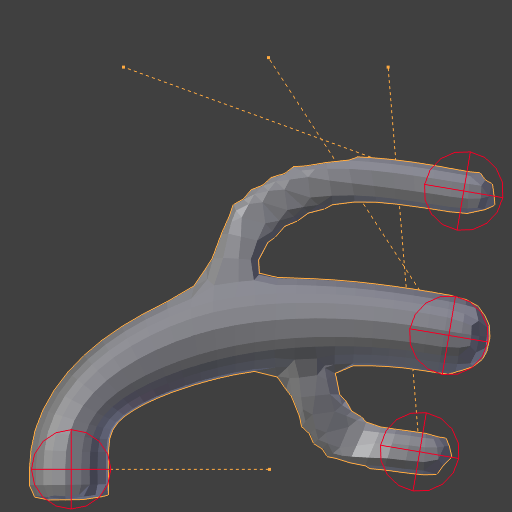
重复操作: 2。¶
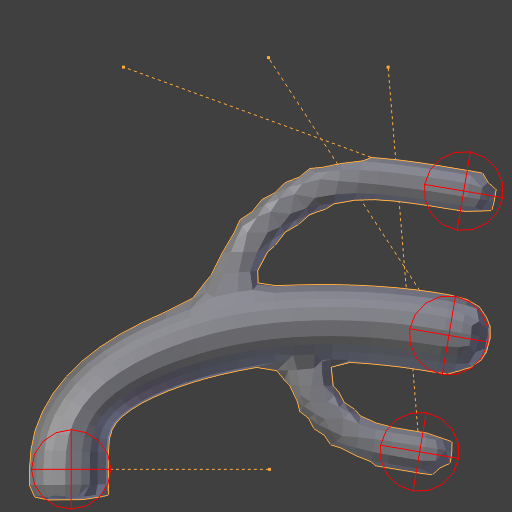
重复: 5.¶

原始模型。¶
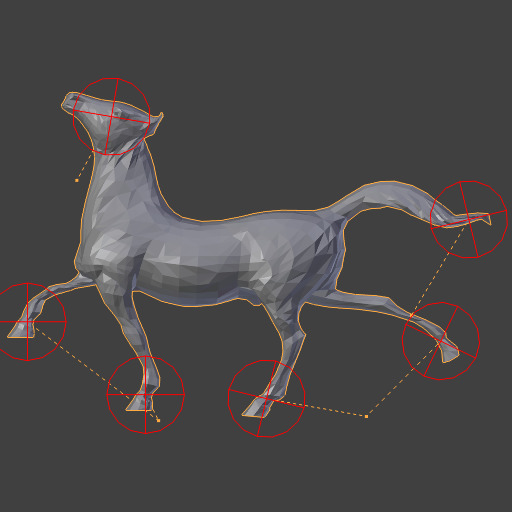
重复: 1.¶
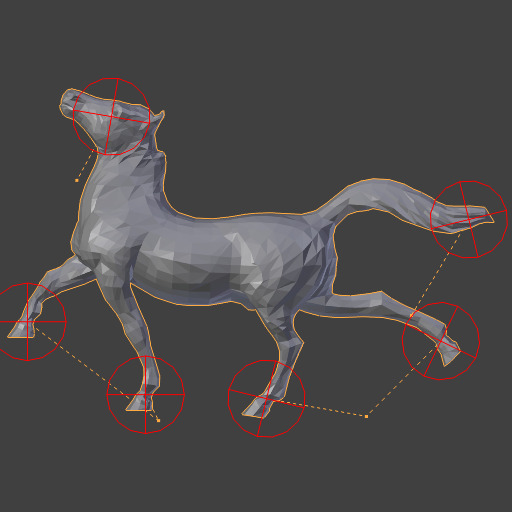
重复操作: 2。¶

重复: 10.¶
- 锚点权重
用户将用于转换模型的顶点组。每个顶点的权值不影响修改器的行为,但该方法只考虑权值大于0的顶点。
- 反转
<-> 反转所选顶点组的影响,这意味着该组现在表示不会被修改器改变形状的顶点。
反转顶点组的权重值。
- 反转
- 绑定
绑定 按钮会告诉 拉普拉斯形变 修改器去获取物体的几何体细节,这使得修改锚点顶点实际上是在修改改变物体的形状。
- 解绑
绑定修改器后, 你可能以后决定更改锚点顶点组,这时,你需要在再一次绑定修改器前 解除绑定 。
错误信息¶
- 顶点组 组名 无效
当用户删除顶点组或当用户更改顶点组的名称,将显示此消息。
- 顶点从X变到Y
当用户添加或删除网格的顶点时,将显示此消息。
- 边从X变到Y
当用户添加或删除网格的边时,将显示此消息。
- 系统找不到解决方案
如果求解器不能找到这个线性系统的解,则显示此消息。
Note
如果网格很密,有100,000以上的顶点,那非线性优化系统很可能会失效。
历史¶
Laplacian Surface Editing is a method developed by Olga Sorkine and others in 2004. This method preserves geometric details as much as possible while the user makes editing operations. This method uses differential coordinates corresponding to the difference between a vector and the weighted average of its neighbors to represent the local geometric detail of the mesh.
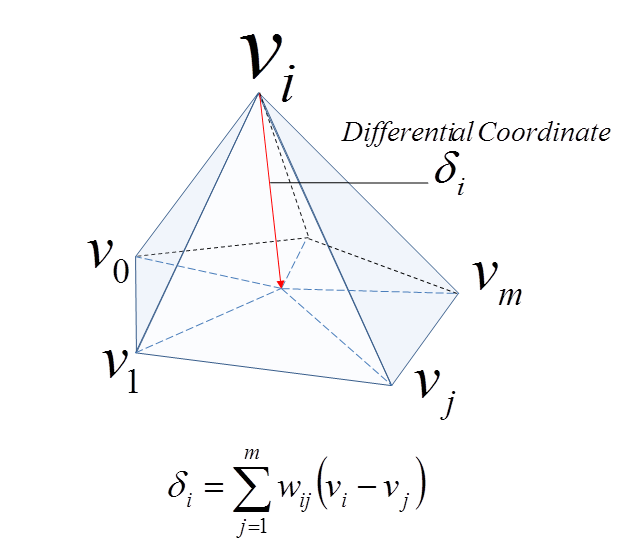
微分坐标。¶
See also