Introduction¶
Après l’animation d’une propriété dans Blender en utilisant des trames clés, vous pouvez éditer leurs courbes correspondantes. Quand quelque chose est « animé », il change au cours du temps. Cette courbe est affichée quelque chose appelée F-curve. De base ce qu’une F-curve fait est une interpolation entre deux propriétés animées. Dans Blender, l’animation d’un objet signifie le changement d’une de ses propriétés, telle que la position de l’objet, ou son échelle.
Comme mentionné, l’unité de temps fondamentale de Blender est la « trame », qui dure habituellement juste une fraction de seconde, selon la fréquence de trame de la scène. Comme l’animation est composée de modifications incrémentales s’étalant sur plusieurs trames, habituellement ces propriétés ne sont pas modifiées manuellement trame par trame, car :
Cela prendrait des lustres !
Il serait très difficile d’obtenir des variations de la propriété (à moins que vous calculiez des fonctions mathématiques et tapiez une valeur précise pour chaque trame, ce qui serait fou).
C’est la raison pour laquelle presque toute l’animation directe est faite en utilisant l”interpolation.
L’idée est simple : vous définissez quelques trames clés, qui sont séparées par plusieurs trames. Entre ces trames clés, les valeurs des propriétés sont calculées (interpolées) par Blender et renseignées. Ainsi, la charge de travail des animateurs est réduite significativement.
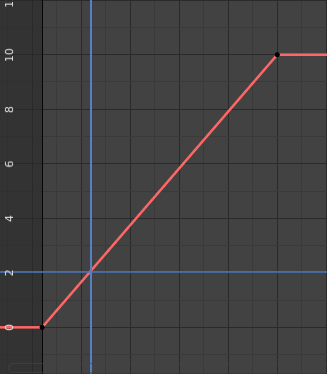
Exemple d’interpolation.¶
Par exemple, si vous avez :
Un point de contrôle de valeur 0 à la trame 0,
un autre de valeur 10 à la trame 25,
et vous utilisez l’interpolation linéaire, puis, à la trame 5, vous obtenez une valeur de 2.
La même chose pour les trames intermédiaires : avec simplement deux points, vous obtenez une augmentation douce de (0 à 10) sur 25 trames. Évidemment, si vous souhaitez que la trame 15 ait une valeur de 9, vous devrez ajouter un autre point de contrôle (ou trame clé)…
Direction de temps¶
Bien que les F-curves soient très semblables au Bézier, il y a quelques différences importantes.
Pour des raisons évidentes, une propriété représentée par une courbe ne peut pas avoir une valeur à un temps donné, par conséquent :
Quand vous déplacez un point de contrôle devant un point de contrôle qui a été précédemment devant le point que vous êtes en train de déplacer, les deux points de contrôle échangent leur ordre dans la courbe éditée, pour éviter que la courbe retourne dans le temps.
Pour la raison ci-dessus, c’est impossible d’avoir une F-curve fermée.
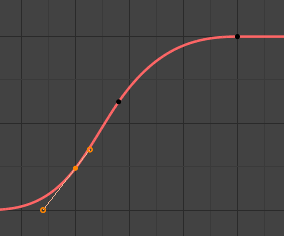
Avant le déplacement de la seconde trame clé.¶ |
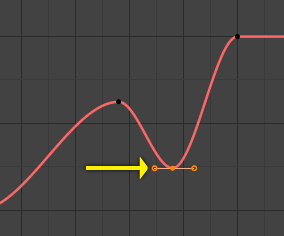
Après le déplacement de la seconde trame clé.¶ |
Réglages¶
Les F-curves ont trois propriétés supplémentaires, qui contrôlent l’interpolation entre les points, le comportement d’extension, et le type de poignées.
Mode d’interpolation¶
Référence
- Menu
- Raccourci
T
Mode pour l”Interpolation entre la trame clé courante et suivante.
Interpolation¶
- Constant
Il n’y a pas d’interpolation du tout. La courbe maintient la valeur de sa dernière trame de référence, en donnant une « courbe » discrète (escalier). Habituellement uniquement utilisé pendant l’étape de « blocage » initiale dans les flux d’animation pose-to-pose.

Constant.¶
- Linear
Cette simple interpolation crée un segment droit, en donnant une ligne non continue. Ce peut être utile quand on utilise seulement deux trames clés et le mode d’extension Extrapolation, pour obtenir facilement une ligne droite infinie (càd. une courbe linéaire).
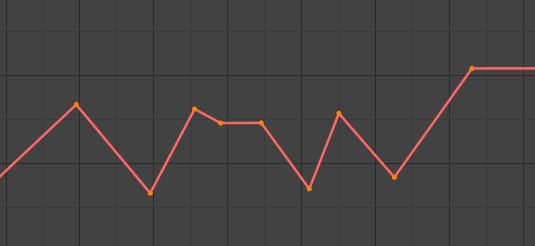
Linear.¶
- Bézier
L’interpolation la plus puissante et la plus utile, et celle par défaut. Elle produit des courbes joliment lissées, càd des animations lisses !
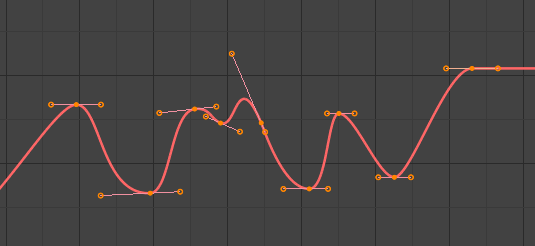
Bézier.¶
Note
Rappelez-vous que certaines F-curves peuvent seulement prendre des valeurs discrètes, auquel cas elles sont toujours affichées comme si c’étaient des constantes interpolées, quelle que soit l’option que vous choisissez.
Accélération (Easing) (par force)¶
Différentes méthodes de courbes d’accélération pour un segment de F-curve. Les « équations d’accélération (easing equations) de Robert Penner » (fondamentalement, des équations qui définissent certaines manières prédéfinies de faire une transition d’une trame clé en une autre) qui réduisent la quantité de travail manuel (insertion et modification des trames clés) pour effectuer certains effets habituels. Par exemple, des mouvements rapides.
Linear
Sinusoidal
Quadratic
Cubic
Quartic
Quintic
Exponential
Circular
Voir aussi
Pour plus d’informations et quelques démos en live, voir https://easings.net et http://www.robertpenner.com/easing/
Effets Dynamiques¶
These additional easing types imitate (fake) physics-based effects like bouncing/springing effects. The corresponding settings can be found in the .
- Elastic
Onde sinusoïdale décroissant exponentiellement, comme une bande élastique. C’est comme plier une perche raide collée à une surface, et la regarder rebondir et à son état d’origine.
- Amplitude
La propriété amplitude contrôle comment l’oscillation diverge de la courbe de base. À 0,0, il n’y a aucune oscillation (càd. elle colle juste à la B-value comme une transition exponentielle extrême), et à 1,0 apparaît un profil comparable à celui affiché dans l’icône.
- Period
La propriété period contrôle la fréquence avec oscillations se produisent. Des valeurs plus élevées produisent des oscillations plus denses.
- Bounce
Rebond parabolique exponentiellement déclinant, comme lors de collisions d’objets. Ex. pour des balles rebondissantes. etc.
- Back
Accélération (easing) cubique avec dépassement et établissement. Utilisez ceci quand vous voulez un peu de dépassement à la prochaine trame clé, ou peut-être pour anticipation.
- Back
La propriété back contrôle la taille et la direction (càd. au dessus/dessous de la courbe) du dépassement.
Easing Type¶
Référence
- Menu
- Raccourci
Ctrl-E
Easing Type contrôle, entre deux trames clés, à quelle extrémité du segment s’appliquent les effets.
- Automatic Easing
Le comportement le plus habituellement attendu parmi ceux ci-dessous est utilisé. Pour les effets de transition, c’est fondamentalement ease in, tandis que pour les effets de physique c’est ease out.
- Ease In
L’effet augmente jusqu’à la seconde trame clé.
- Ease Out
L’effet s’estompe à partir de la première trame clé.
- Ease In Out
L’effet se produit aux deux extrémités du segment.
Extrapolation Mode¶
Référence
- Menu
- Raccourci
Maj-E
Extrapolation définit le comportement d’une courbe avant la première trame clé et après la dernière.
Il y a deux modes d’interpolation de base :
- Constant
Celui par défaut, les courbes avant leur première trame clé et après leur dernière ont une valeur constante (celle des première et dernière trames clés).
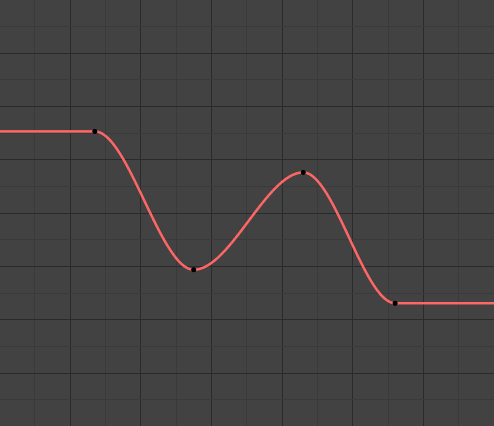
Extrapolation constante.¶
- Linear
Les extrémités des courbes sont des lignes droites (linéaires), comme définies par la pente de leurs première et dernière trames clés.
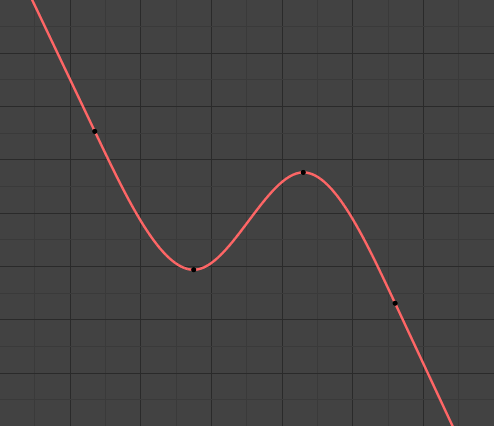
Extrapolation linéaire.¶
Outils d’extrapolation supplémentaires (ex. le modificateur de Cycles) se trouvent dans Modificateurs de F-curve.
Handle Type¶
Référence
- Menu
- Raccourci
V
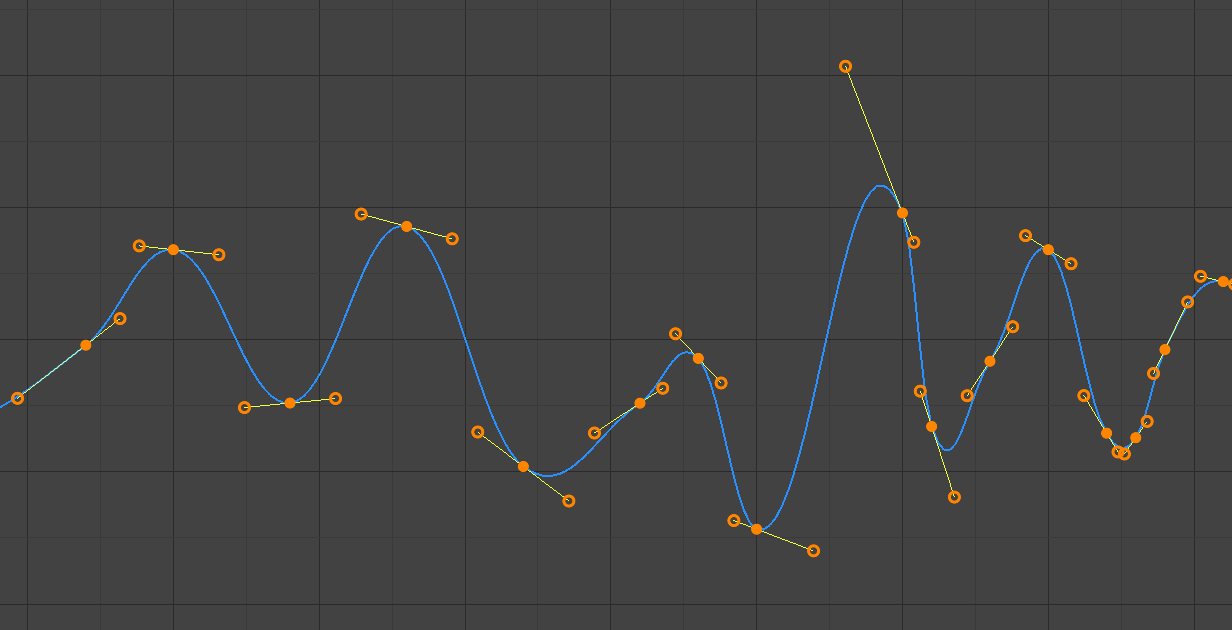
En utilisant les courbes interpolées de Bézier, il est possible de contrôler la pente de la courbe aux points de contrôle. Cela se fait via les poignées des points de courbe ; vous pouvez définir le type de poignée à utiliser pour les points de courbe en appuyant sur V ou en choisissant Key, Handle Type dans le menu de l’éditeur de Graphe. Chaque point de courbe peut avoir un type de poignée différent, même à l’intérieur d’une même courbe.
Il existe trois modes automatiques, Automatic, Auto Clamped, et Vector, dans lesquels Blender détermine automatiquement la pente de la courbe à chaque point de contrôle. Les points de contrôle voisins ont la plus grande influence de la pente, et les points plus éloignés ont une influence plus faible. Ceci peut être contrôlé par F-curve avec les propriétés Auto Handle Smoothing.
En utilisant les autres modes, non automatiques, vous avez un contrôle manuel total sur la pente.
- Automatic
Les positions des poignées sont automatiquement choisies pour produire des courbes lisses.
Poignées Auto.¶
- Auto Clamped
Poignées automatiques serrées pour éviter les dépassements et les changements de direction de la courbe entre les trames clés (en forme de S).
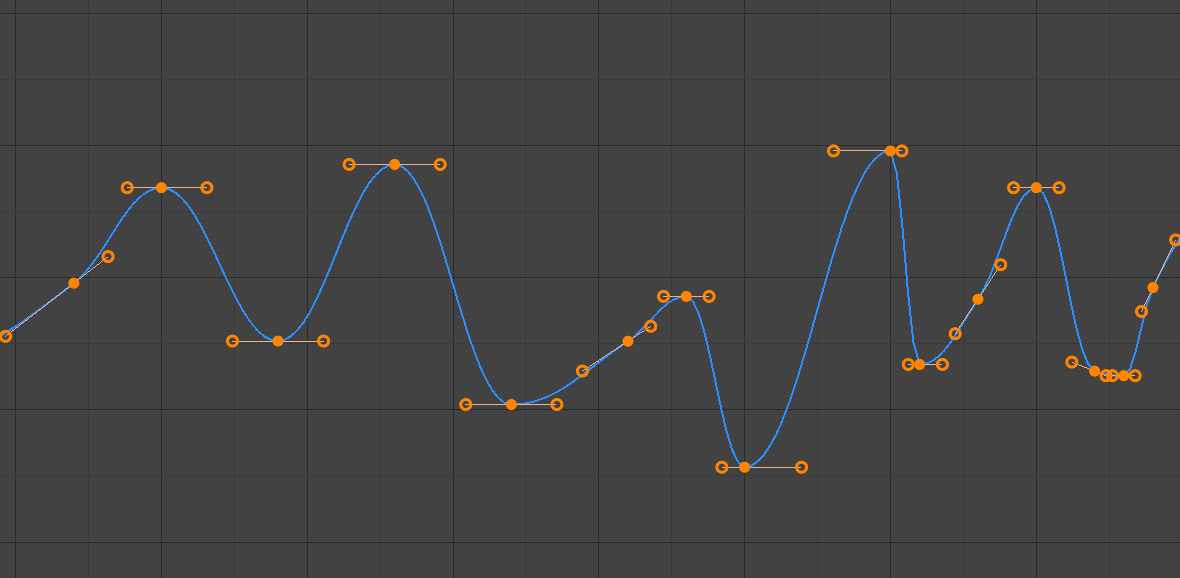
Poignées Auto serrées.¶
- Vector
Crée une interpolation linéaire automatique entre les trames clés. Les segments linéaires restent si le centre des trames clés sont déplacés. Si une poignée est déplacée, elle devient libre (Free).
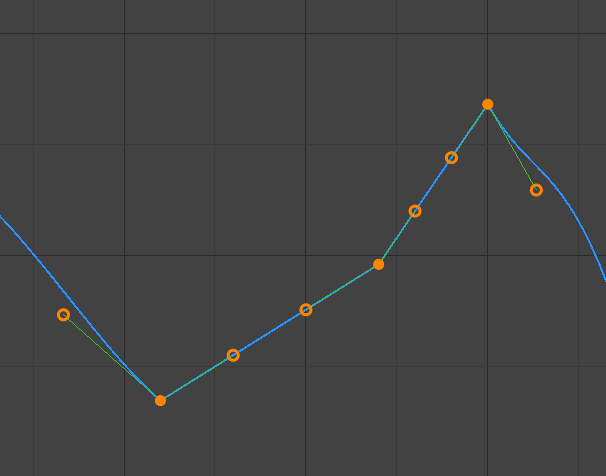
Poignées Vector.¶
- Aligned
Les deux poignées du point de courbe sont verrouillées ensemble pour toujours pointer dans des directions exactement opposées. Il en résulte une courbe qui est toujours lisse au point de contrôle.
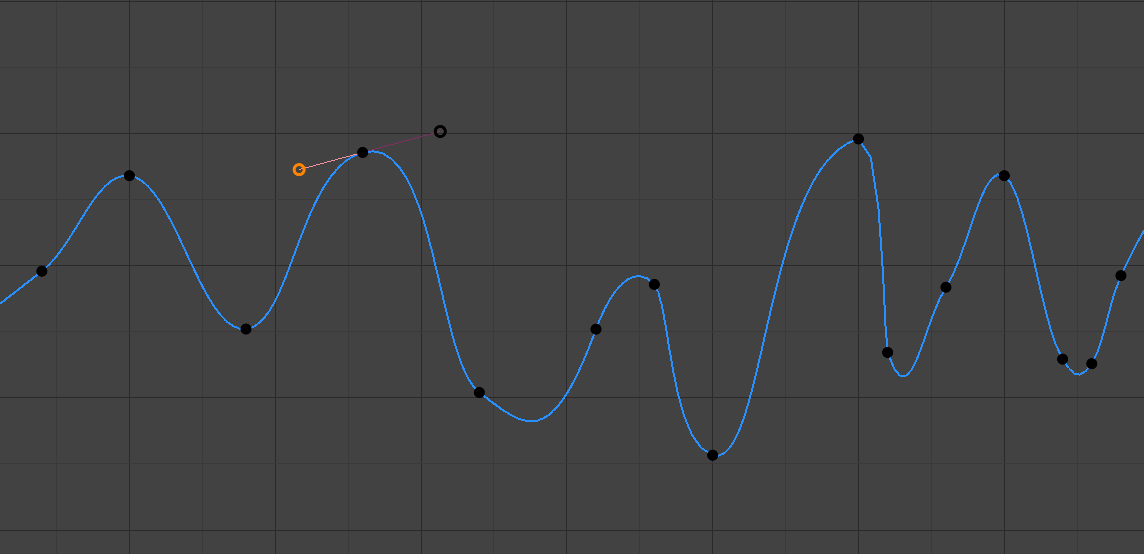
Poignées Aligned.¶
- Free
Les poignées peuvent être déplacées de manière totalement indépendante, ce qui peut entraîner un brusque changement de direction.
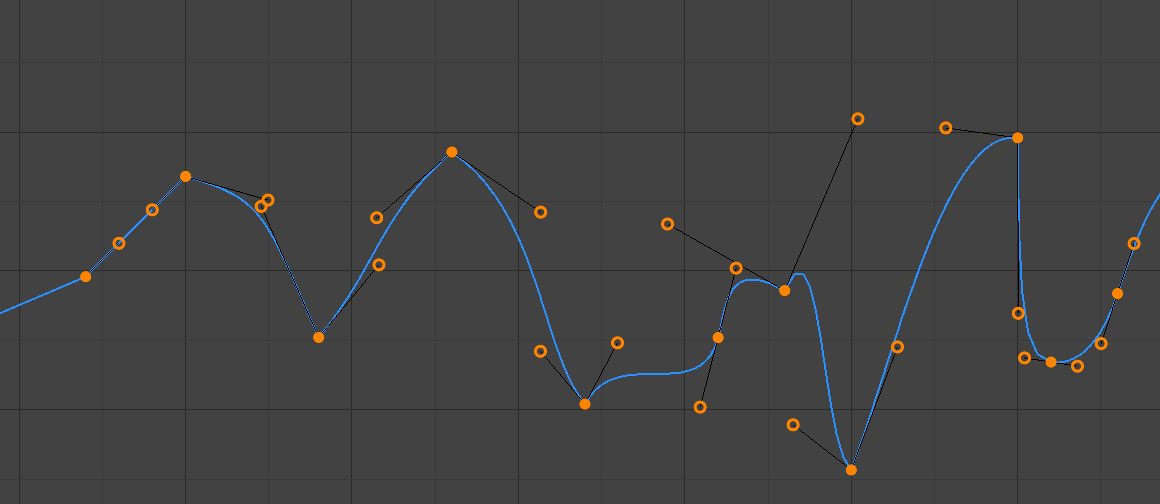
Poignées Free.¶