Nœud Voronoi Texture
Le nœud Voronoi Texture évalue un Bruit de Worley aux coordonnées de la texture d’entrée.
Entrées
Les entrées sont dynamiques, elles deviennent disponibles si nécessaire en fonction des propriétés du nœud.
- Vector
Coordonnées de la texture pour évaluer le bruit ; par défaut, les coordonnées de la texture générée si le socket n’est pas connecté.
- W
Coordonnée de la texture pour évaluer le bruit.
- Scale
L’échelle du bruit.
- Smoothness
La douceur du bruit.

Smoothness: 0.0.

Smoothness: 0.25.

Smoothness: 0.5.

Smoothness: 1.0.

Smoothness: 0.0.

Smoothness: 0.25.

Smoothness: 0.5.

Smoothness: 1.0.
- Exponent
Exposant de la métrique de distance de Minkowski.

Exponent: 0.5.

Exponent: 1.0.

Exponent: 2.0.

Exponent: 32.0.
- Randomness
Le caractère aléatoire du bruit.

Randomness: 1.0.

Randomness: 0.5.

Randomness: 0.25.

Randomness: 0.0.
Propriétés
- Dimensions
Les dimensions de l’espace dans lequel on évalue le bruit.
- 1D
Évaluer le bruit dans l’espace 1D à l’entrée W.
- 2D
Évaluer le bruit dans l’espace 2D au niveau de l’entrée Vector. Le composant Z est ignoré.
- 3D
Évaluer le bruit dans l’espace 3D au niveau de l’entrée Vector.
- 4D
Évaluer le bruit dans l’espace 4D au niveau de l’entrée Vector et l’entrée W comme quatrième dimension.
Des dimensions plus élevées correspondent à un temps de rendu plus important. Il convient donc d’utiliser des dimensions plus faibles, sauf si des dimensions plus élevées sont nécessaires.
- Feature
L’élément de Voronoï que le nœud va calculer.
- F1
La distance au point caractéristique le plus proche ainsi que sa position et sa couleur.

Distance.

Color.

Position.
- F2
La distance au deuxième point caractéristique le plus proche ainsi que sa position et sa couleur.

Distance.

Color.

Position.
- Smooth F1
Une version lisse de F1.

Distance.

Color.

Position.
- Distance to Edge
La distance aux bords des cellules Voronoi.

Distance.

Distance inférieure à 0.05.
- N-Sphere Radius
Le rayon de la n-sphère inscrite dans les cellules de Voronoï. En d’autres termes, il s’agit de la moitié de la distance entre le point caractéristique le plus proche et le point caractéristique le plus proche de lui.

Le rayon n-sphère peut être utilisé pour créer des n-sphères étroitement emballées.
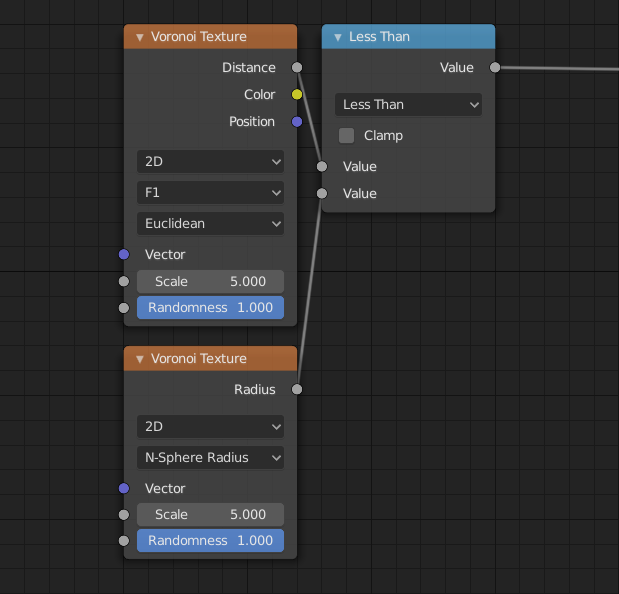
Arbre de nœuds pour le shader à gauche.
- Distance Metric
La distance métrique utilisée pour calculer la texture.
- Euclidean
Utiliser Euclidean distance metric.
- Manhattan
Utiliser Manhattan distance metric.
- Chebychev
Utiliser Chebychev distance metric.
- Minkowski
Utiliser la Minkowski distance metric. La distance de Minkowski est une généralisation des métriques susmentionnées avec un exposant comme paramètre. Minkowski avec un exposant de un est équivalent à la métrique de distance de Manhattan. Minkowski avec un exposant de deux est équivalent à la métrique de distance euclidienne. Minkowski avec un exposant infini est équivalent à la métrique de distance Chebychev.

Exposant Minkowski: 0,5 (Minkowski 1/2).

Exposant Minkowski: 1.0 (Manhattan).

Exposant Minkowski: 2.0 (Euclidien).

Exposant Minkowski: 32.0 (approximation de Tchebychev).
Sorties
- Distance
Distance.
- Color
Couleur de la cellule. La couleur est arbitraire.
- Position
Position du point caractéristique.
- W
Position du point caractéristique.
- Radius (rayon)
Rayon N-sphère.
Notes
Dans certaines configurations du nœud, notamment pour de faibles valeurs de Randomness, des artefacts de rendu peuvent se produire. Cela se produit pour les mêmes raisons que celles décrites dans la section Notes de la page White Noise Texture et peut être corrigé de manière similaire à ce qui y est décrit.
Exemples
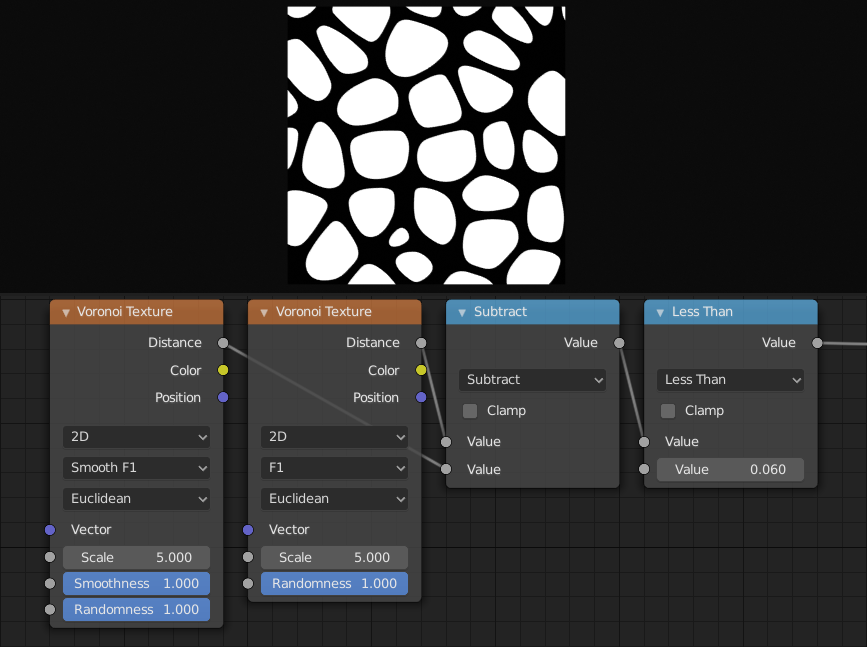
La différence entre F1 et Smooth F1 peut être utilisée pour créer des cellules de Voronoï biseautées.
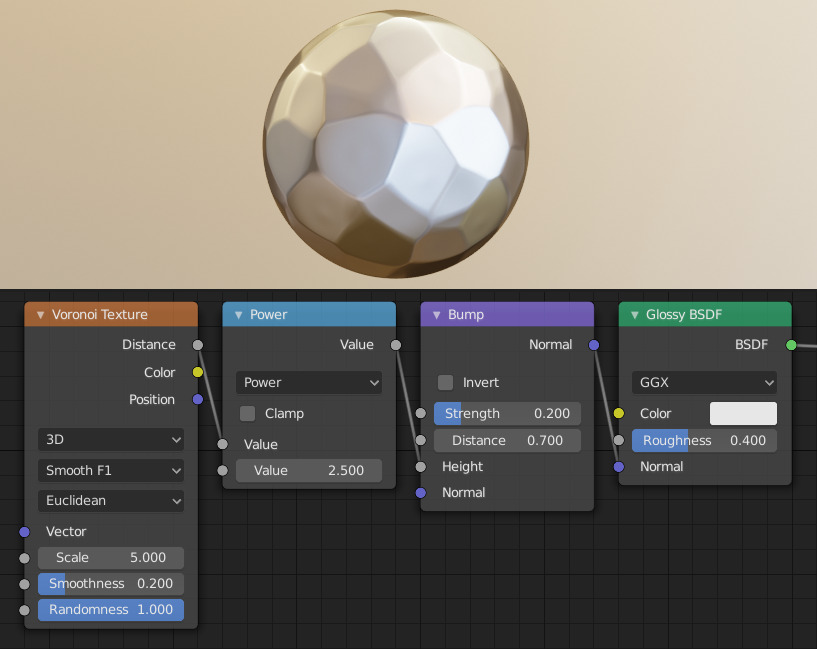
Création d’un shader en métal martelé à l’aide du nœud Texture Voronoi.