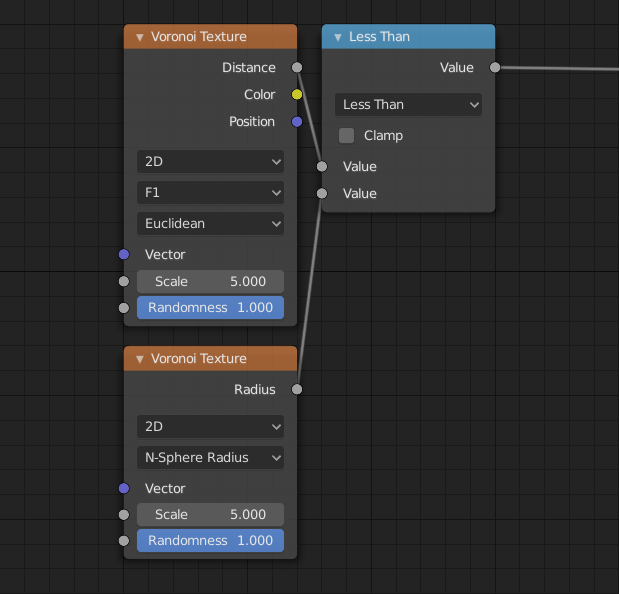
沃罗诺伊纹理
沃罗诺伊纹理 节点在输入纹理坐标处评估 Worley噪波。
输入
输入是动态的，下面的输入端口会在选择的节点属性需要时出现。
属性
- 维度
用于计算噪波的空间维度。
- 1D:
在输入W处评估一维空间的噪声。
- 2D:
评估输入矢量处 2D 空间中的噪声。Z 分量将被忽略。
- 3D:
在输入矢量处评估三维空间的噪声。
- 4D:
在4D空间中评估输入Vector和输入W为第四维的噪声。
更高的维度对应着更高的渲染时间，所以除非有必要使用更高的维度，否则应该使用更低的维度。
- 特性
节点将要计算的沃罗诺伊的特性。
- 间隔矩阵
用于计算纹理的距离度量。
- 欧几里德:
使用 欧氏距离度量。
- 曼哈顿点距:
使用 曼哈顿距离度量。
- 切比雪夫:
使用 切比切夫距离度量。
- 闵可夫斯基:
使用 Minkowski距离度量。闵可夫斯基距离是上述度量的一个泛化，有一个 指数 作为参数。指数为1的Minkowski等同于 Manhattan 距离度量。指数为二的Minkowski相当于 欧几里得 距离度量。指数为无限的Minkowski相当于 Chebychev 距离度量。
闵可夫斯基指数: 0.5（闵可夫斯基 1/2）。
闵可夫斯基指数: 1.0（曼哈顿）。
闵可夫斯基指数: 2.0（欧几里得）。
闵可夫斯基指数: 32.0（切比雪夫近似）。
输出
- 距离
距离。
- 颜色
单元格颜色。颜色是任意的。
- 位置
特征点的位置。
- W
特征点的位置。
- 半径
N维球面半径。
注意
在节点的某些配置中，特别是对于 随机性 的低值，可能会出现渲染伪影。发生这种情况的原因与白噪波纹理页面中的 注意章节 中描述的原因相同，并且可以以与此处描述类似的方式进行修复。
示例
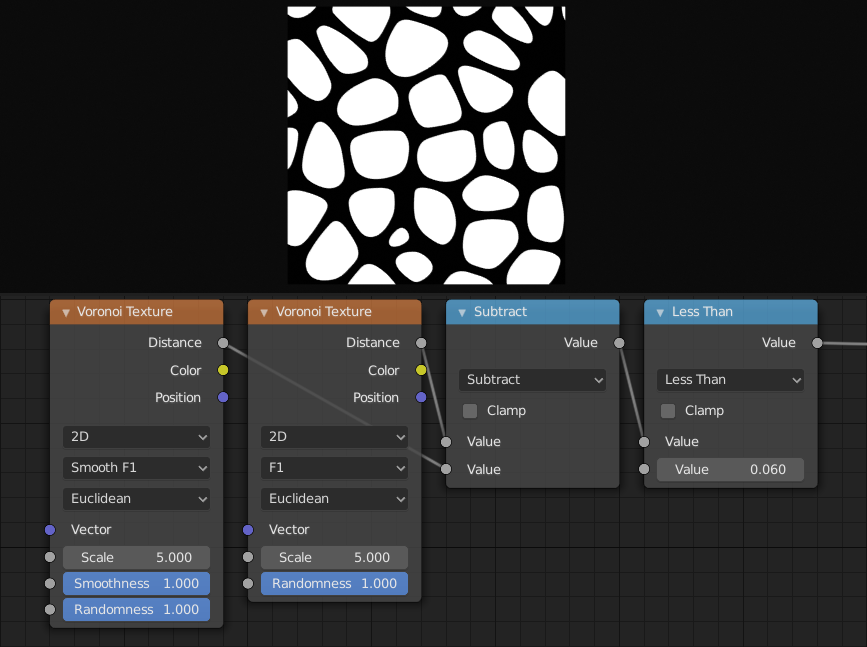
F1 和 平滑 F1 之间的差异可以用来创建斜面的沃罗诺伊单元。
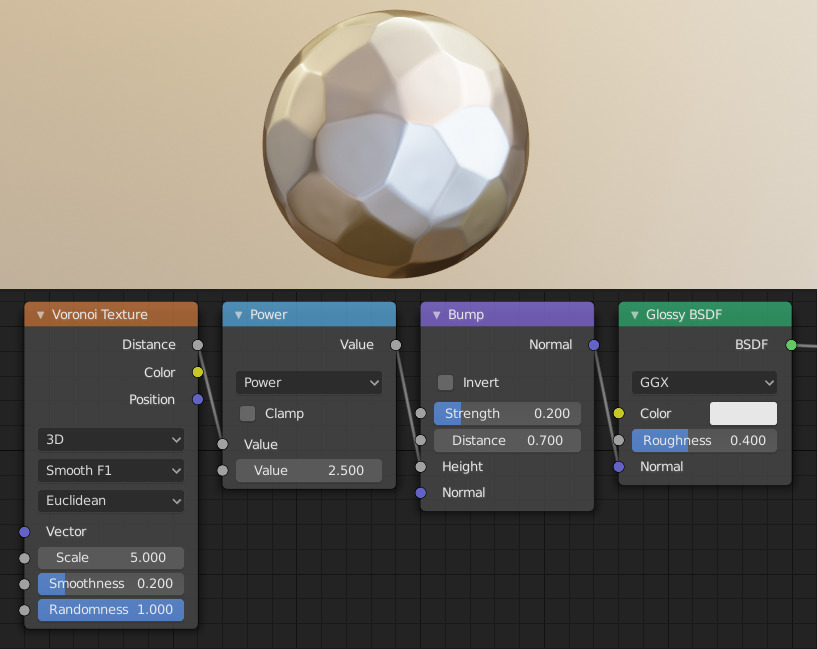
使用 沃罗诺伊纹理 节点创建一个锤击的金属着色器。