Node Voronoi Texture

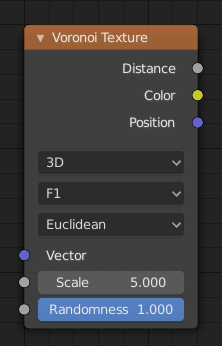
../../../_images/render_shader-nodes_textures_voronoi_node.png

Node Voronoi Texture.

The Voronoi Texture node evaluates a Worley Noise at the input texture coordinates.

Entrées

The inputs are dynamic, they become available if needed depending on the node properties.

Vector
Texture coordinate to evaluate the noise at; defaults to Generated texture coordinates if the socket is left unconnected.
W
Texture coordinate to evaluate the noise at.
Scale
Scale of the noise.
Smoothness

The smoothness of the noise.

../../../_images/render_shader-nodes_textures_voronoi_smoothness_distance_zero.png

Smoothness: 0.0.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_distance_quarter.png

Smoothness: 0.25.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_distance_half.png

Smoothness: 0.5.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_distance_one.png

Smoothness: 1.0.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_color_zero.png

Smoothness: 0.0.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_color_quarter.png

Smoothness: 0.25.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_color_half.png

Smoothness: 0.5.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_color_one.png

Smoothness: 1.0.
Exponent

Exponent of the Minkowski distance metric.

../../../_images/render_shader-nodes_textures_voronoi_minkowski_half.png

Exponent: 0.5.
../../../_images/render_shader-nodes_textures_voronoi_minkowski_one.png

Exponent: 1.0.
../../../_images/render_shader-nodes_textures_voronoi_minkowski_two.png

Exponent: 2.0.
../../../_images/render_shader-nodes_textures_voronoi_minkowski_32.png

Exponent: 32.0.
Randomness

The randomness of the noise.

../../../_images/render_shader-nodes_textures_voronoi_randomness_one.png

Randomness: 1.0.
../../../_images/render_shader-nodes_textures_voronoi_randomness_half.png

Randomness: 0.5.
../../../_images/render_shader-nodes_textures_voronoi_randomness_quarter.png

Randomness: 0.25.
../../../_images/render_shader-nodes_textures_voronoi_randomness_zero.png

Randomness: 0.0.

Propriétés

Dimensions

The dimensions of the space to evaluate the noise in.

1D
Evaluate the noise in 1D space at the input W.
2D
Evaluate the noise in 2D space at the input Vector. The Z component is ignored.
3D
Evaluate the noise in 3D space at the input Vector.
4D
Evaluate the noise in 4D space at the input Vector and the input W as the fourth dimension.

Higher dimensions corresponds to higher render time, so lower dimensions should be used unless higher dimensions are necessary.

Feature

The Voronoi feature that the node will compute and return.

F1

Compute and return the distance to the closest feature point as well as its position and color.

../../../_images/render_shader-nodes_textures_voronoi_smoothness_distance_zero.png

Distance.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_color_zero.png

Color.
../../../_images/render_shader-nodes_textures_voronoi_f1_position.png

Position.
F2

Compute and return the distance to the second closest feature point as well as its position and color.

../../../_images/render_shader-nodes_textures_voronoi_f2_distance.png

Distance.
../../../_images/render_shader-nodes_textures_voronoi_f2_color.png

Color.
../../../_images/render_shader-nodes_textures_voronoi_f2_position.png

Position.
Smooth F1

Compute and return a smooth version of F1.

../../../_images/render_shader-nodes_textures_voronoi_smoothness_distance_one.png

Distance.
../../../_images/render_shader-nodes_textures_voronoi_smoothness_color_one.png

Color.
../../../_images/render_shader-nodes_textures_voronoi_smooth_f1_position.png

Position.
Distance To Edge

Compute and return the distance to the edges of the Voronoi cells.

../../../_images/render_shader-nodes_textures_voronoi_distance-to-edge.png

Distance.
../../../_images/render_shader-nodes_textures_voronoi_distance-to-edge_less-than.png

Distance < 0.05.
N-Sphere Radius

Compute and return the radius of the n-sphere inscribed in the Voronoi cells. In other words, it is half the distance between the closest feature point and the feature point closest to it.

../../../_images/render_shader-nodes_textures_voronoi_n-sphere-radius.png

The n-sphere radius can be used to create tightly packed n-spheres.
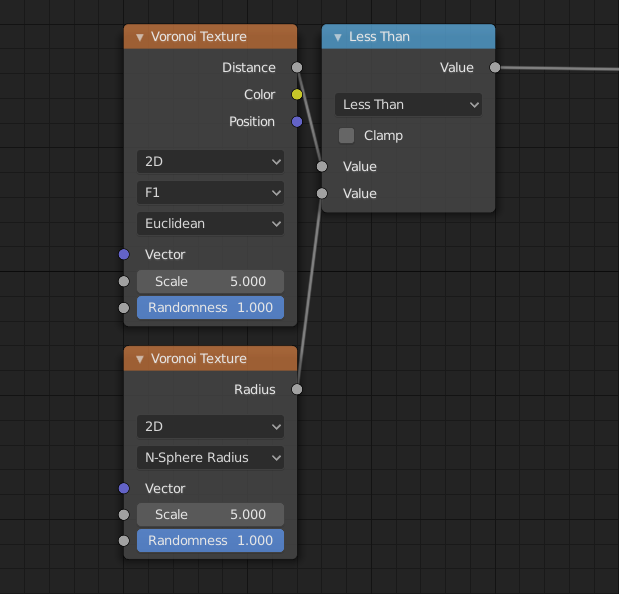
../../../_images/render_shader-nodes_textures_voronoi_n-sphere-radius_nodetree.png

Node tree for the shader to the left.
Distance Metric

The distance metric used to compute the texture.

Euclidean
Use the Euclidean distance metric.
Manhattan
Use the Manhattan distance metric.
Chebychev
Use the Chebychev distance metric.
Minkowski
Use the Minkowski distance metric. The Minkowski distance is a generalization of the aforementioned metrics with an Exponent as a parameter. Minkowski with an exponent of one is equivalent to the Manhattan distance metric. Minkowski with an exponent of two is equivalent to the Euclidean distance metric. Minkowski with an infinite exponent is equivalent to the Chebychev distance metric.
../../../_images/render_shader-nodes_textures_voronoi_minkowski_half.png

Minkowski Exponent: 0.5 (Minkowski 1/2).
../../../_images/render_shader-nodes_textures_voronoi_minkowski_one.png

Minkowski Exponent: 1.0 (Manhattan).
../../../_images/render_shader-nodes_textures_voronoi_minkowski_two.png

Minkowski Exponent: 2.0 (Euclidean).
../../../_images/render_shader-nodes_textures_voronoi_minkowski_32.png

Minkowski Exponent: 32.0 (approximation of Chebychev).

Sorties

Distance
Distance.
Color
Cell color. The color is arbitrary.
Position
Position of feature point.
W
Position of feature point.
Radius
N-Sphere radius.

Exemples

../../../_images/render_shader-nodes_textures_voronoi_example_beveled_cells.png

The difference between F1 and Smooth F1 can be used to create beveled Voronoi cells.

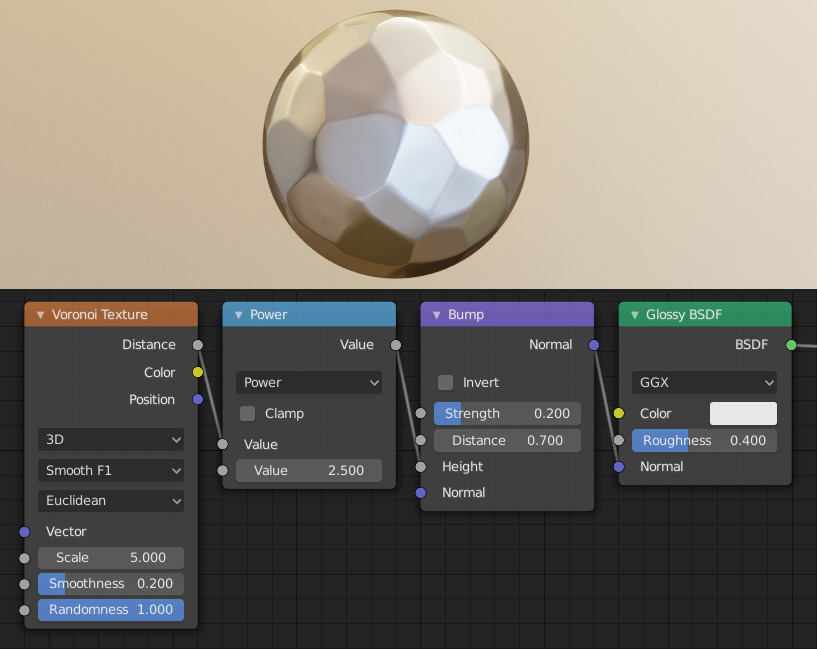
../../../_images/render_shader-nodes_textures_voronoi_example_hammered_metal.jpg

Creating a hammered metal shader using the Voronoi Texture node.