Structure¶
Nombre de concepts de courbes, en particulier ceux de NURBS, sont directement transposables sur les surfaces NURBS, tels que les points de contrôle, Order, Weight, Resolution, etc. Ici nous ne discuterons que des différences.
Il est très important de comprendre la différence entre les courbes NURBS et les surfaces NURBS : les premières ont une dimension, les autres en ont deux. Blender traite en interne Les surfaces NURBS et les courbes NURBS complètement différemment. Il y a plusieurs attributs qui les différencient mais le plus important est qu’une courbe NURBS a un seul axe d’interpolation (U) et une surface NURBS a deux axes d’interpolation (U et V).
Cependant, vous pouvez avoir des surfaces « 2D » faites de courbes (en utilisant les outils d’extrusion, ou, à un moindre degré, le remplissage de courbes 2D fermées). Et vous pouvez avoir des courbes « 1D » faites de surfaces, comme une surface NURBS avec seulement une rangée (dans la direction U ou V) de points de contrôle produit seulement une courbe…
Visuellement, vous pouvez savoir lequel est lequel en entrant en Mode Édition et en regardant l’entête de la Vue 3Dt : soit l’entête affiche Surface ou Curve comme l’un des choix de menu. Vous pouvez également extruder une courbe de surface NURBS entière pour créer une surface, mais vous ne pouvez pas avec une simple courbe NURBS.
Points de contrôle, lignes et grille¶
Les points de contrôle des surfaces NURBS sont les mêmes que pour les courbes NURBS. Cependant, leur disposition est assez contraignante. Le concept de « segment » disparaît, remplacé par celui de « lignes » et de « grille » globale.
Une « rangée » (row) est un ensemble de points de contrôle formant une « ligne » dans une direction d’interpolation (un peu semblable à des edge loops pour les maillages). Ainsi vous avez des « rangées-U » et des « rangées-V » dans une surface NURBS. Le point clé est que toutes les rangées d’un type donné (U ou V) ont le même nombre de points de contrôle. Chaque point de contrôle appartient exactement à une rangée-U et à une rangée-V.
Tout cela forme une « grille » ou « cage », dont la forme contrôle la forme de la surface NURBS. Un peu comme un lattice…
Il est très important de comprendre : vous ne pouvez pas ajouter un point de contrôle unique à une surface NURBS ; vous devez ajouter une ligne U ou V entière (en pratique, vous utiliserez l’outil Extrude, ou peut-être l’outil Duplicate, pour en ajouter…), contenant exactement le même nombre de points que les autres. Cela signifie aussi que vous ne serez capable de « fusionner » différentes portions de surfaces que si au moins une de leurs lignes se correspond.
Poids¶
Semblable aux NURBS Splines NURBS Les points de contrôle de surface ont une propriété de poids. Cette propriété de poids contrôle l’influence du point de contrôle sur la surface. Ce poids ne doit pas être confondu avec le Goal Weight, qui n’est utilisé que pour les simulations de corps mou. Le poids du point de contrôle NURBS peut être ajusté dans le champ numérique W du Transform panel.
Dans Fig. Un point de contrôle avec un poids de 5. un seul point de contrôle, portant l’étiquette « C », a eu son poids (Weight) fixé à 5.0 alors que tous les autres ont leur valeur par défaut de 1.0. Comme vous pouvez le voir, ce point de contrôle « tire » la surface vers lui.
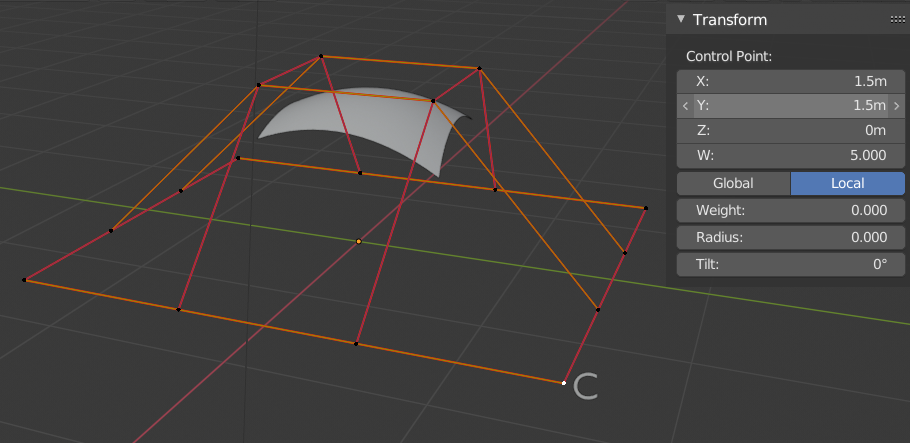
Un point de contrôle avec un poids de 5.¶
Note
Si tous les points de contrôle ont le même poids alors ils s’annulent mutuellement. C’est la différence dans les poids qui fait que la surface se déplace vers ou s’éloigne d’un point de contrôle.
Preset Weights¶
Les NURBS peuvent créer des formes pures telles que des cercles, des cylindres et des sphères (notez qu’un cercle de Bézier n’est pas un cercle pur). Pour créer des cercles, des sphères ou des cylindres purs, vous devez définir des valeurs spécifiques pour les poids des points de contrôle. Ce n’est pas intuitif, et vous devriez lire plus sur les NURBS avant d’essayer cela.
Pour créer une sphère avec des surfaces 2D, c’est le même principe qu’avec un cercle 2D. Vous noterez les quatre différents poids nécessaires pour créer une sphère (1.0, 0.707 = sqrt(0.5), 0.354 = sqrt(2)/4, et 0.25).
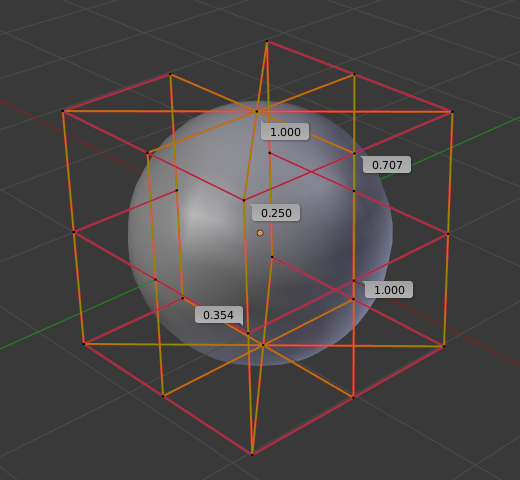
Une surface sphèrique.¶