Active Spline

Reference

Mode:

編輯模式

選單:

Properties ‣ Curve ‣ Active Spline

See also

Active Spline for curves.

The Active Spline panel is used in Edit Mode to control properties of the currently selected spline.

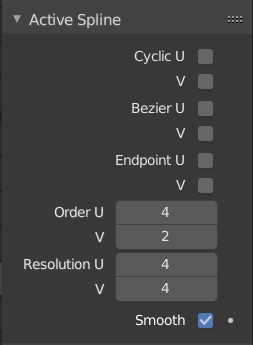
../../../_images/modeling_surfaces_properties_active-spline_panel.png

Active Spline panel.

Cyclic U/V

Like curves, surfaces can be closed (cyclical) or open, independently in both directions, allowing you to easily create a tube, torus or sphere shape, and they can be viewed as "solids" in Edit Mode. This can be set per interpolation axis.

Bézier U

Makes the surface act like a Bézier curve. The control points act like Free handles of a Bézier curve. Depending on the Order, 3 or 4 control points form one spline segment. This can be set per interpolation axis.

Endpoint U/V

Makes the surface contact the end control points. This can be set per interpolation axis.

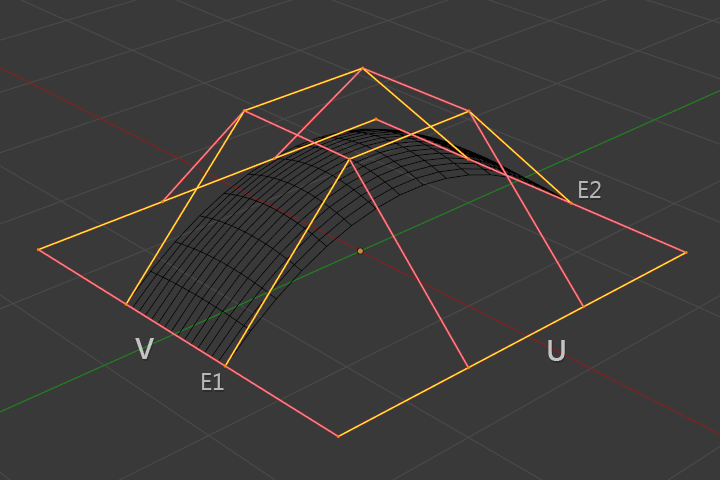
../../../_images/modeling_surfaces_properties_active-spline_endpoint.png

Endpoint U.

In the image below, the U interpolation axis is labeled as "U" and the V interpolation axis is labeled as "V". The U's interpolation axis has been set to Endpoint and as such the surface now extends to the outer edges from E1 to E2 along the U interpolation axis.

To cause the surface to extend to all edges, Endpoint would be set for the V's axis as well.

Order U/V

This property is the same as with NURBS Curves; it specifies how much the control points are taken into account for calculating the curve of the surface shape. For high Orders 1 the surface pulls away from the control points, creating a smoother surface by assuming that the Resolution U/V is high enough. For lowest Orders 2 the surface follows the control points, creating a surface that tends to follow the grid cage.

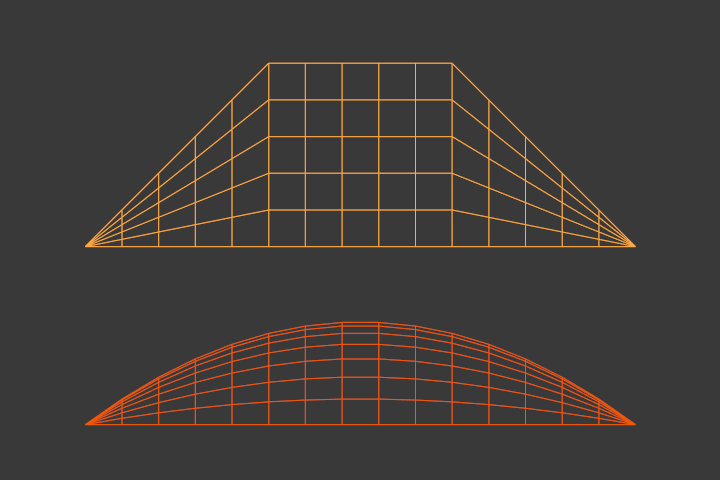
../../../_images/modeling_surfaces_properties_active-spline_order.png

Order 2 and Order 4 surface.

For illustration purposes, in both Fig. Order 2 and Order 4 surface., the knot vectors were set to Endpoint, causing the surface to extend to all edges.

You can set independently the order for each interpolation axis, and like curves, it cannot be lower than 2, and higher than 6 or the number of control points on the relevant axis.

Resolution U/V

Alters the resolution of each segment by changing the number of subdivisions. This can be set per interpolation axis.

Smooth

Use Smooth Shading for any 3D geometry.