Edges of Vertex Node

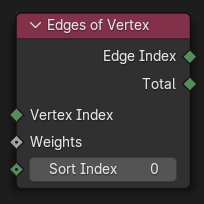
Edges of Vertex node.

Selects a neighboring edge of a vertex and outputs its index.

This node is a bit special because it operates in two different domains. First, it evaluates a Weight for each edge in the geometry. Then, for each item in the context domain, it will:

  • Pick a vertex from the geometry based on the Vertex Index.

  • Find the edges connected to this vertex.

  • Sort these edges by their associated weight.

  • Pick an edge from the above sorted list based on the Sort Index, where 0 means the edge with the lowest weight, 1 means the edge with the second-lowest weight and so on.

  • Output the geometry-wide index of this edge.

Inputs

Vertex Index

The index of the vertex for which to find the edges.

Catatan

If this input is not connected, it uses the index of the context item, which means it's important that the node is evaluated in the Point domain.

Weights

The weights of the edges in the geometry. Unlike the other inputs which follow the context domain, this one is always evaluated in the Edge domain.

The edges are sorted by their associated weight in ascending order. Edges with the same weight are sorted by their index.

Sort Index

The 0-based index of the edge to select from the vertex's sorted edges. If this value is outside the range of valid indices, it wraps around.

Properti

This node has no properties.

Outputs

Edge Index

The geometry-wide index of the selected edge. You can pass this to the Evaluate at Index Node or the Sample Index Node (with the domain set to Edge) to retrieve details about the edge.

If the vertex has no connected edges, Edge Index will be zero.

Total

The number of edges connected to the selected vertex.

Example

The example below creates a cone at each vertex of a "cube," aligned to the neighboring edge that's the most vertical.

First, we calculate a "verticality score" for each of the cube's edges. To do this, we subtract the positions of its vertices to get its direction vector, which we normalize and use to calculate the dot product with the Z axis. The absolute value of that gives us a number between 0 and 1, where 0 means fully horizontal and 1 means fully vertical.

Because the edges will be sorted by ascending weight, we set weight = 1 - verticality. This way, the most vertical connected edge of each vertex will have the lowest weight and come first in the list.

Next, in the point domain, we need to calculate the rotation of each cone. By using the Align Rotation to Vector Node, the problem gets simplified and we only need to calculate a direction vector.

The direction vector of each cone is the centerpoint of the most vertical neighboring edge minus the position of the vertex. Finding that most vertical neighboring edge is where the Edges of Vertex node comes in: for each vertex, it sorts the connected edges by their weight and pick the first one (because the Sort Index is 0). Once we have the edge's index, we use the Evaluate at Index Node to retrieve its centerpoint.

With the rotations of the cones calculated, we use the Instance on Points Node to create them.

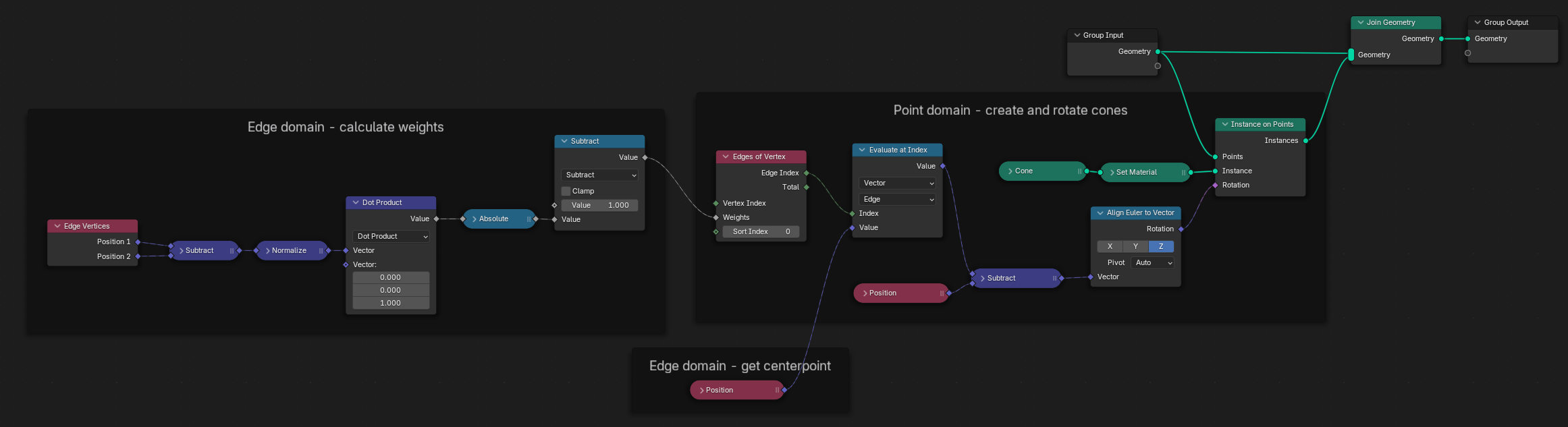
../../../../_images/modeling_geometry-nodes_mesh_topology_edges-of-vertex_example-setup.png

Example node setup. (Rightclick and choose "Open image in new tab" to see a larger version.)

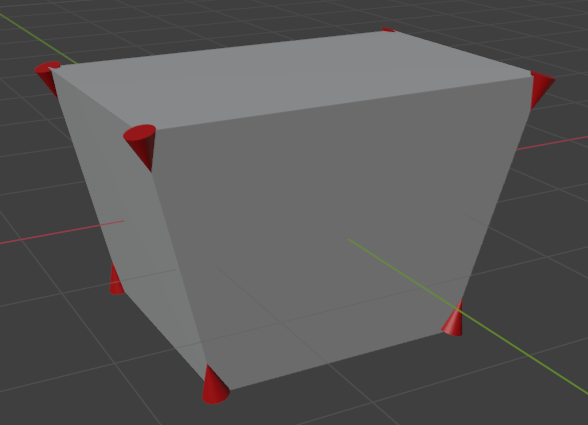
../../../../_images/modeling_geometry-nodes_mesh_topology_edges-of-vertex_example-result.png

The resulting geometry.