Узел «Векторная математика»

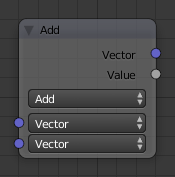
Узел «Векторная математика»

Узел «Векторная математика» выполняет указанное математическое преобразование над векторами. Выберите математическую функцию из выпадающего списка, в котором показано значение «Добавить».

Входы

Вектор

Входной вектор 1 (верхний). Значение предоставляется другим узлом или указывается вручную.

Вектор

Входной вектор 2 (нижний). Значение предоставляется другим узлом или указывается вручную.

Свойства

Операция

Select the math function for conversion.

Добавить

Складывает входы 1 и 2.

Подсказка

\[ \begin{align}\begin{aligned}Vector &= input_1 + input_2\\Value &= \frac{abs(Vector_x) + abs(Vector_y) + abs(Vector_z)} {3.0}\end{aligned}\end{align} \]

Вычесть

Вычитает вход 1 из входа 2.

Подсказка

\[ \begin{align}\begin{aligned}Vector &= input_1 - input_2\\Value &= \frac{abs(Vector_x) + abs(Vector_y) + abs(Vector_z)} {3.0}\end{aligned}\end{align} \]

Средний

Усредняет входы 1 и 2.

Подсказка

\[ \begin{align}\begin{aligned}Vector &= \frac{input_1+input_2} {|input_1+input_2|}\\Value &= |input_1+input_2|\end{aligned}\end{align} \]

Скал. произведение

Алгебраическая операция, принимающая две равных по длине последовательности векторов и возвращающая одно число. В результате на выходе получается скалярное значение.

Подсказка

\[Value = input_1 . input_2\]

Вект. произведение

Геометрическая бинарная операция над двумя векторами в трёхмерном пространстве. В результате получается вектор, перпендикулярный обоим входным векторам, то есть, нормаль к содержащей их плоскости. В результате на выходе получается вектор.

Подсказка

\[ \begin{align}\begin{aligned}Vector &= \frac{input_1 \times input_2} {|input_1 \times input_2|}\\Value &= |input_1 \times input_2|\end{aligned}\end{align} \]

Нормализовать

Normalizing input 1.

Подсказка

\[ \begin{align}\begin{aligned}Vector &= \frac{input_1} {|input_1|}\\Value &= |input_1|\end{aligned}\end{align} \]

Выходы

Вектор

Выходной вектор, получающийся после преобразования узла.

Значение

Выходное значение, получающееся после преобразования узла.