Structure¶
Muitos dos conceitos das curvas, especialmente as aplicáveis as curvas NURBS, também se aplicam diretamente as superfícies NURBS, como os conceitos sobre os pontos de controle, Ordem, Pesos de influência, Resolução, etc. Aqui nesta página, nós iremos simplesmente falar sobre as diferenças entre elas.
É muito importante entender a diferença entre as curvas NURBS e as superfícies NURBS: A primeira possui apens uma dimensão, e a segunda possui duas. O Blender trata internamente as superfícies NURBS e as curvas NURBS de maneira completamente diferenciada. Existem muitos atributos que as separam mas o mais importante é que uma curva NURBS possui um único eixo de interpolação (U) e a superfície NURBS possui dois eixos de interpolação (U e V).
Contudo, você pode ter superfícies «2D» compostas de curvas (usando as ferramentas de extrusão, ou, em uma extensão ainda menor, o preenchimento de curvas 2D fechadas). E você pode ter curvas «1D» compostas de superfícies, como uma as superfícies NURBS compostas de apenas uma linha (tanto na direção U quanto V) pois os pontos de controle produzem apenas uma curva…
Visually you can tell which is which by entering Edit Mode and looking at the 3D Viewport header: either the header shows Surface or Curve as one of the menu choices. Also, you can extrude a whole NURBS surface curve to create a surface, but you cannot with a simple NURBS curve.
Pontos de controle, Linhas e Grade¶
Os pontos de controle para as superfícies NURBS são os mesmos disponíveis para as curvas NURBS. Contudo, o seu esquema de funcionamento é bem mais restrito. O conceito de «segmento» desaparece, e é substituído pelas «linhas» e pela «grade» geral.
A «row» is a set of control points forming one «line» in one interpolation direction (a bit similar to edge loops for meshes). So you have «U rows» and «V rows» in a NURBS surface. The key point is that all rows of a given type (U or V) have the same number of control points. Each control point belongs to exactly one U row and one V row.
All this forms a «grid», or «cage», the shape of which controls the shape of the NURBS surface. A bit like a lattice…
This is very important to grasp: you cannot add a single control point to a NURBS surface; you have to add a whole U or V row at once (in practice, you will usually use the Extrude tool, or perhaps the Duplicate one, to add those…), containing exactly the same number of points as the others. This also means that you will only be able to «merge» different pieces of surfaces if at least one of their rows matches together.
Weight¶
Similar to NURBS Splines NURBS Surface control points have a weight property. This weight property controls how much influence the control point has on the surface. This weight should not be confused with the Goal Weight, which is used only for soft body simulations. The NURBS control point weight can be adjusted in the W number field of the Transform panel.
Na imagem Um dos pontos de controle com um peso de influência de 5., um único ponto de controle, rotulado como «C», teve seu Peso de influência definido para 5.0 enquanto todos os outros permanecem em seu padrão de 1.0. Como você pode ver, este ponto de controle puxa a superfície em direção a si.
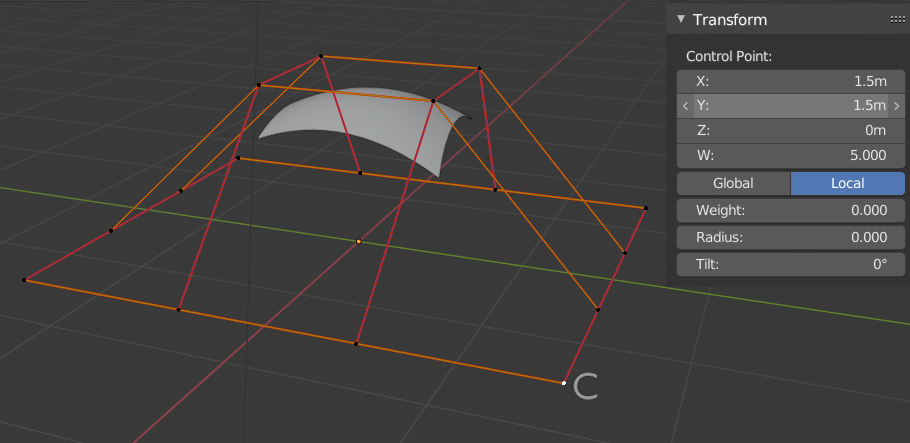
Um dos pontos de controle com um peso de influência de 5.¶
Nota
Caso todos os pontos de controle tenham os mesmos Pesos de influência, então cada um deles cancelará a saída dos outros. Esta é a diferença nos pesos que fazem com que a superfície se mova para mais próximo ou mais distante de cada ponto de controle.
Predefinições de pesos de influência¶
NURBS can create pure shapes such as circles, cylinders, and spheres (note that a Bézier circle is not a pure circle). To create pure circles, spheres, or cylinders, you must set to specific values the weights of the control points. This is not intuitive, and you should read more on NURBS before trying this.
Para criar uma esfera através de superfícies 2D, podem ser usados os mesmos princípios de um círculo 2D. Você irá notar que os quatro pesos de influência diferentes necessários para a criação da esfera são (1.0, 0.707 = sqrt(0.5), 0.354 = sqrt(2)/4, e 0.25), onde sqrt é a raiz quadrada.
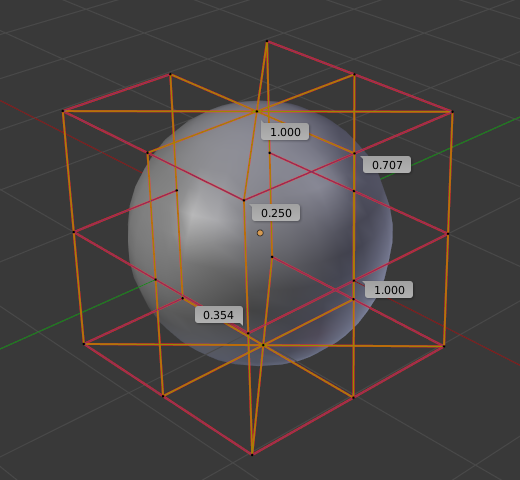
Uma superfície de esfera.¶