Remesh Modifier

The Remesh modifier is a tool for generating new mesh topology. The output follows the surface curvature of the input, but its topology contains only quads.

Options

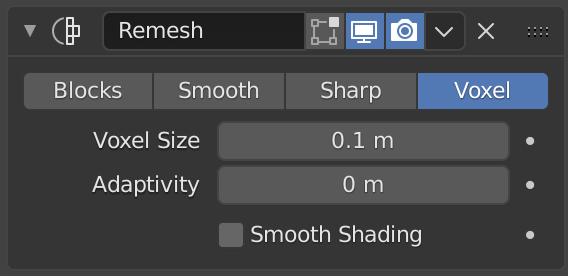
../../../_images/modeling_modifiers_generate_remesh_panel.png

The Remesh modifier.

Mode

There are three basic modes available in the Remesh modifier. The output topology is almost identical between the three modes, what changes is the smoothing.

Blocks

There is no smoothing at all.

Smooth

Output a smooth surface.

Sharp

Similar to Smooth, but preserves sharp edges and corners.

Sharpness

Higher values produce edges more similar to the input, while lower values filter out noise.

Voxel

Uses an OpenVDB to generate a new manifold mesh from the current geometry while trying to preserve the mesh’s original volume.

Adaptivity

Reduces the final face count by simplifying geometry where detail is not needed. This introduce triangulation to faces that do not need as much detail.

Smooth Shading

Outputs faces with Smooth Shading instead of flat shading.

Octree Depth

Sets the resolution of the output. Low values will generate larger faces relative to the input, higher values will generate a denser output.

축척(Scale)

The result can be tweaked further by this, lower values effectively decrease the output resolution.

Remove Disconnected

Filter out small disconnected pieces of the output.

Thin parts of the input mesh can become loose, and generate small isolated bits of mesh. This option will remove those.

Threshold

Use this to control how small a disconnected component must be to be removed.

Smooth Shading

Output faces with smooth shading rather than flat shading. The smooth/flat shading of the input faces is not preserved.

참고

The input mesh should have some thickness to it. If the input is completely flat, add a Solidify Modifier above the Remesh one.

예시

../../../_images/modeling_modifiers_generate_remesh_example-none.png

Unmodified mesh.
../../../_images/modeling_modifiers_generate_remesh_example-blocks-depth-3.png

Blocks mode with Octree Depth 3.
../../../_images/modeling_modifiers_generate_remesh_example-smooth-depth-3.png

Smooth mode with Octree Depth 3.
../../../_images/modeling_modifiers_generate_remesh_example-sharp-depth-2.png

Sharp mode with Octree Depth 2.
../../../_images/modeling_modifiers_generate_remesh_example-sharp-depth-3.png

Sharp mode with Octree Depth 3.
../../../_images/modeling_modifiers_generate_remesh_example-sharp-depth-4.png

Sharp mode with Octree Depth 4.
../../../_images/modeling_modifiers_generate_remesh_example-text-topology.png

The Remesh Modifier applied to a text to improve its topology.

Animated Example