Nodo Operar (vectores)¶
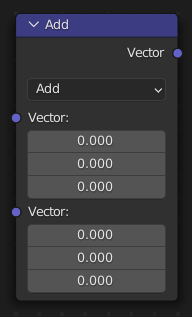
El nodo Operar (vectores) permitirá realizar una variedad de operaciones matemáticas sobre los vectores de entrada.
Entradas¶
Las entradas del nodo son dinámicas. Algunas entradas sólo estarán disponibles durante ciertas operaciones. Por ejemplo, la entrada Escala sólo estará disponible al usar la operación Escalar.
- Vector
El vector de entrada \(A = \begin{pmatrix} A_x \\ A_y \\ A_z \end{pmatrix}\).
- Vector
El vector de entrada \(B = \begin{pmatrix} B_x \\ B_y \\ B_z \end{pmatrix}\).
- Escala
Entrada de Escala \(s\).
Propiedades¶
- Operación
La operación vectorial a ser aplicada sobre los vectores de entrada.
- Agregar:
La suma de A y B. \(\begin{pmatrix} A_x + B_x \\ A_y + B_y \\ A_z + B_z \end{pmatrix}\)
- Sustraer:
La diferencia entre A y B. \(\begin{pmatrix} A_x - B_x \\ A_y - B_y \\ A_z - B_z \end{pmatrix}\)
- Multiplicar:
El producto Hadamard entre A y B. \(\begin{pmatrix} A_x \cdot B_x \\ A_y \cdot B_y \\ A_z \cdot B_z \end{pmatrix}\)
- Dividir:
La división Hadamard entre A y B. Una división entre cero dará por resultado cero. \(\begin{pmatrix} A_x / B_x \\ A_y / B_y \\ A_z / B_z \end{pmatrix}\)
- Multiplicar Adicionar:
La combinación Hadamard de las operaciones multiplicar y adicionar. \(A × B + C\)
- Producto vectorial:
El producto vectorial de A y B. \(\begin{pmatrix} A_y \cdot B_z - A_z \cdot B_y \\ A_z \cdot B_x - A_x \cdot B_z \\ A_x \cdot B_y - A_y \cdot B_x \end{pmatrix}\)
- Proyectar (o Proyecto):
La proyección de A sobre B.
- Reflejar:
La reflexión de A en torno a la normal B. B no necesitará estar normalizada.
- Refractar:
Para un vector incidente A, una normal de superficie B y una tasa de índices de refracción (IR), producirá el vector de refracción R.
- Hacia adelante:
Orientará un vector A para que apunte alejándose de una superficie B según la normal indicada C. Calculará \((dot(B, C) < 0) ? A : -A\).
- Producto escalar:
El producto escalar de A y B. \(A_x \cdot B_x + A_y \cdot B_y + A_z \cdot B_z\)
- Distancia:
La distancia entre A y B.
- Longitud:
La longitud de A. \(\sqrt{A_x^2 + A_y^2 + A_z^2}\)
- Escala:
El resultado de multiplicar A por el valor de entrada escalar Escala. \(\begin{pmatrix} s \cdot A_x \\ s \cdot A_y \\ s \cdot A_z \end{pmatrix}\)
- Normalizar:
El resultado de normalizar A. El vector resultante apuntará en la misma dirección que A y tendrá una longitud de 1. Si A fuera (0, 0, 0), el resultado también sería (0, 0, 0).
- Envolver (o Ciclo):
El resultado Hadamard de un valor entre Mín y Máx, basado en la diferencia absoluta entre el valor de entrada y el múltiplo entero más cercano de Máx menor que el valor.
- Adherir:
El resultado de redondear A al máximo múltiplo entero de B menor o igual a A.
- Piso:
Redondeará el valor de entrada al entero Hadamard inferior más cercano.
- Techo:
Redondeará el valor de entrada al entero Hadamard superior más cercano.
- Resto:
El resto Hadamard de A dividido B.
- Fracción:
Devolverá la parte fraccionaria Hadamard del valor.
- Absoluto:
El valor absoluto Hadamard de A.
- Mínimo:
El valor mínimo Hadamard entre A y B.
- Máximo:
El valor máximo Hadamard entre A y B.
- Seno:
El Seno <https://es.wikipedia.org/wiki/Seno_(trigonometr%C3%ADa)> Hadamard de A.
- Coseno:
El Coseno <https://es.wikipedia.org/wiki/Coseno> Hadamard de A.
- Tangente:
La Tangente <https://es.wikipedia.org/wiki/Tangente_(trigonometr%C3%ADa)> Hadamard de A.
Salidas¶
La salida del nodo será dinámica. Podrá tratarse de un vector o un valor escalar, dependiendo de la operación que esté siendo ejecutada. Por ejemplo, la operación Longitud producirá una salida escalar, mientras que la operación Adicionar producirá una vectorial.
- Vector
Vector de salida.
- Valor
Valor de salida.