Limit Location Constraint¶
An object or unconnected bone can be moved around the scene along the X, Y and Z axes. This constraint restricts the amount of allowed translations along each axis, through lower and upper bounds.
The limits for an object are calculated from its origin, and the limits of a bone, from its root.
It is interesting to note that even though the constraint limits the visual and rendered location of its owner, its owner's data-block still allows (by default) the object or bone to have coordinates outside the minimum and maximum ranges. This can be seen in its Transform panel.
When an owner is selected and attempted to be moved outside the limit boundaries, it will be constrained to those boundaries visually and when rendered, but internally, its coordinates will still be changed beyond the limits. If the constraint is removed, its ex-owner will seem to jump to its internally specified location.
Similarly, if its owner has an internal location that is beyond the limits, dragging it back into the limit area will appear to do nothing until the internal coordinates are back within the limit threshold (unless you enabled the Affect Transform option, see below).
Setting equal the min and max values of an axis, locks the owner's movement along that axis... Although this is possible, using the Transformation Properties axis locking feature is probably easier!
Options(オプション)¶
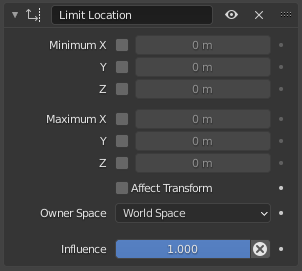
Limit Location panel.¶
- Minimum X, Y, Z
These buttons enable the lower boundary for the location of the owner's origin along, respectively, the X, Y and Z axes of the chosen Space. The number field below them controls the value of their limit. Note that if a min value is higher than its corresponding max value, the constraint behaves as if it had the same value as the max one.
- Maximum X, Y, Z
These buttons enable the upper boundary for the location of the owner's origin along, respectively, the X, Y and Z axes of the chosen Space. Same options as above.
- Affect Transform
As pointed out before by default, even though visually constrained, the owner can still have coordinates out of bounds (as shown by the Transform panel). Well, when you enable this checkbox, this is no longer possible -- the owner's transform properties are also limited by the constraint. However, note that, the constraint does not directly modify the coordinates: you have to select its owner one way or another for this to take effect...
- Owner
This constraint allows you to choose in which space to evaluate its owner's transform properties. See common constraint properties for more information.
- Influence(影響)
Controls the percentage of affect the constraint has on the object. See common constraint properties for more information.