Noise Texture (ノイズテクスチャ)ノード#
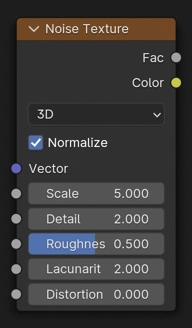
The Noise Texture node evaluates a fractal Perlin noise at the input texture coordinates. It can be used for a single Perlin noise evaluation, or for combining multiple octaves (layers) with increasingly finer detail.
入力#
入力は動的であり、ノードのプロパティに応じて、使用可能になります。
- Vector(ベクトル)
ノイズを評価するテクスチャ座標。ソケットが接続されていない場合、デフォルトは生成されたテクスチャ座標です。
- W
ノイズを評価するテクスチャ座標。
- Scale(スケール)
ベースノイズオクターブのスケール。
- Detail (細かさ)
ノイズのオクターブの数。入力の小数部には、最高オクターブの大きさが乗算されます。オクターブ数が多いほど、レンダリング時間が長くなります。
- Roughness
Blend between a smoother noise pattern, and rougher with sharper peaks.
- Lacunarity (空隙性)
連続する2つのオクターブのスケールの差。値が大きく、オクターブが高いほどスケールが大きくなります。
- Offset(オフセット)
各オクターブに追加されたオフセット、最高値のオクターブが現れるレベルを決定します。
- Gain(ゲイン)
オクターブの大きさを調整するための追加の乗数。
- Distortion(歪み)
Amount of distortion.
Properties(プロパティ)#
- Dimensions(寸法)
ノイズを評価する次元スペース。
- 1D:
入力 W で1D空間のノイズを評価します。
- 2D:
入力 Vector で2D空間のノイズを評価します。Zコンポーネントは無視されます。
- 3D:
入力 Vector で3D空間のノイズを評価します。
- 4D:
4番目の次元として、 Vector 入力とベクトルと W 入力で4D空間のノイズを評価します。
注釈
Higher dimensions corresponds to higher render time, so lower dimensions should be used unless higher dimensions are necessary.
- Normalize(正規化)
If enabled, ensures that the output values stay in the range 0.0 to 1.0. When disabled, output values are in the range -1.0 to 1.0.
- Type(タイプ)
Type of Noise texture, with different ways to combine octaves.
- FBM:
Fractal Brownian motion, produces a homogeneous and isotropic result. Values from octaves are added together.
- Multifractal (マルチフラクタル):
More uneven, varying by location similar to real terrain. Values from octaves are multiplied together.
- Hybrid Multifractal (ハイブリッド マルチフラクタル):
Creates peaks and valleys with different roughness values, like real mountains rise out of flat plains. Combines octaves using both addition and multiplication.
- Ridged Multifractal (畝のある マルチフラクタル):
鋭い峰を作成します。ノイズの絶対値を計算して "渓谷" を作成し、サーフェスを上下逆にします。
- Hetero Terrain:
Hybrid Multifractalと同様に、不均一な地形を作成しますが、河川の道のようです。
出力#
- Factor(係数)
フラクタルノイズの値
- Color(カラー)
各コンポーネントごとの異なるフラクタルノイズカラー
例#
詳細なNoise Texture。#
ノート#
While the noise is random in nature, it follows a certain pattern that might not evaluate to random values in some configurations. For instance, consider the following configuration where a grid of objects have a material that evaluates a noise texture at their locations. One might expect the objects to have random values since they have different locations, but this is not the case.
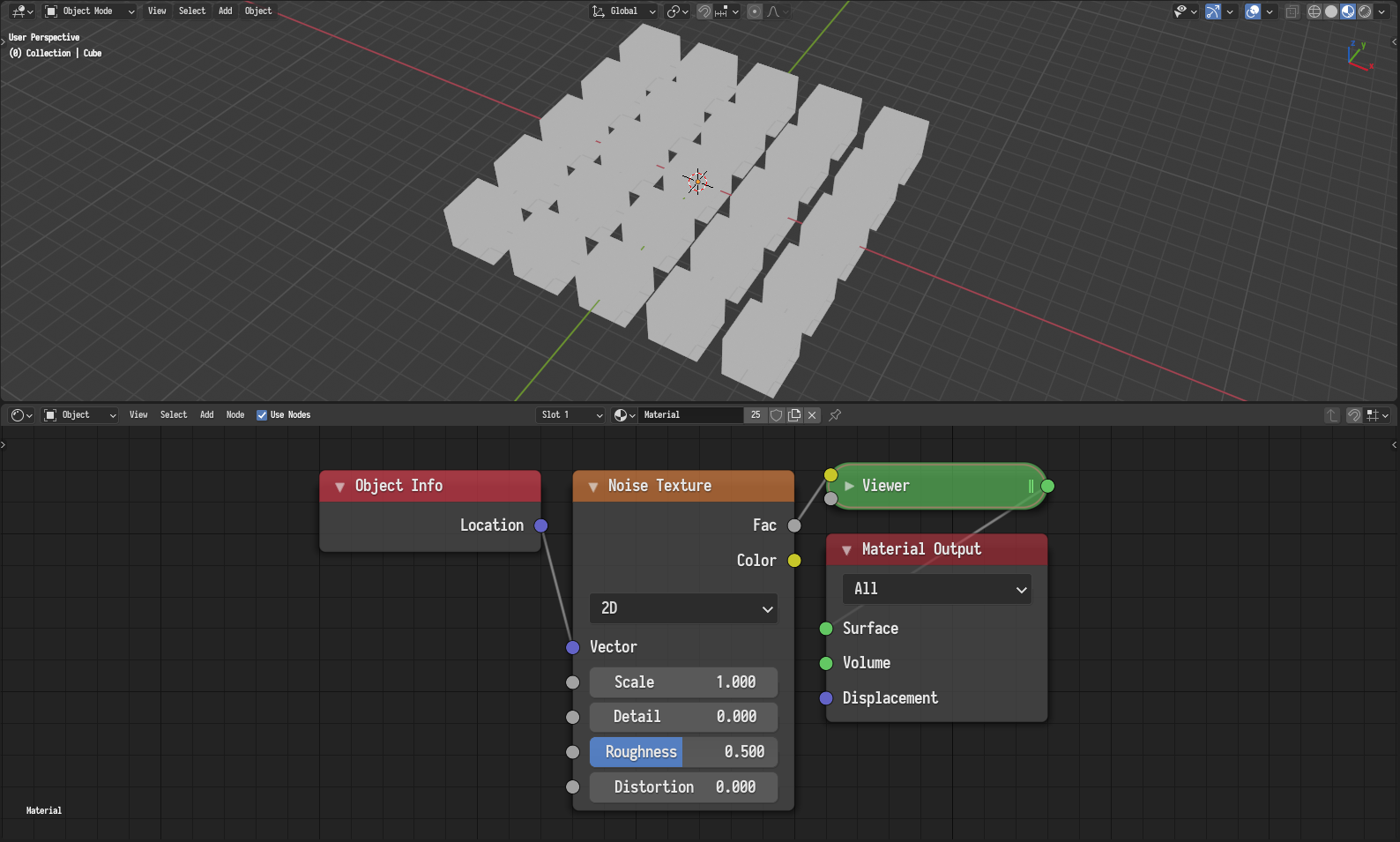
An example configuration where the noise evaluates to a constant value.#
It seems all objects have a value of 0.5. To understand why this happens, let us look at the following plot of a 1D noise texture.
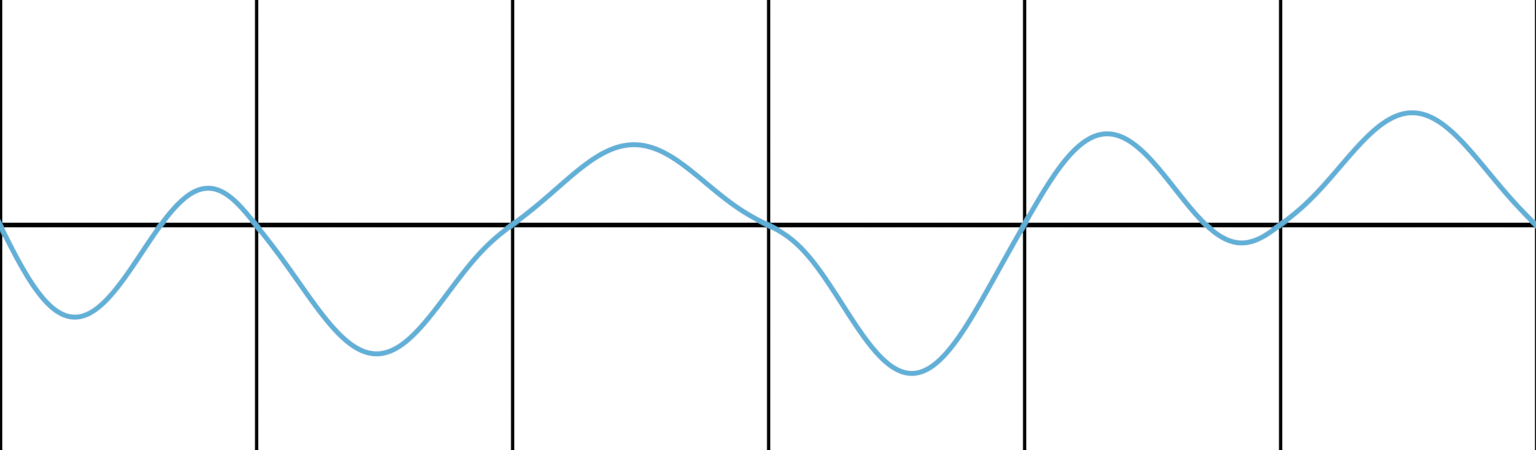
A plot of a 1D noise with zero details and zero distortion.#
The horizontal line denotes a value of 0.5 and the vertical lines denotes whole numbers assuming a noise scale of 1. As can be seen, the noise always intersects the 0.5 line at whole numbers. Since the aforementioned objects were distributed on a grid and have whole number locations, they all evaluate to 0.5. Which explains the issue at hand.
Generally, any discrete evaluation of noise at integer multiples of the reciprocal of the noise scale will always evaluate to 0.5. It also follows that evaluations closer to that will have values close to 0.5. In such cases, it is almost always preferred to use the White Noise Texture.
Regardless, one can mitigate this issue in a number of ways:
Adjust the scale of the noise to avoid aligning the noise with the evaluation domain.
Add an arbitrary offset to the texture coordinates to break the alignment with the evaluation domain.
Evaluate the noise at a higher dimension and adjust the extra dimension until a satisfactory result is achieved.
|
Constant value issue.# |
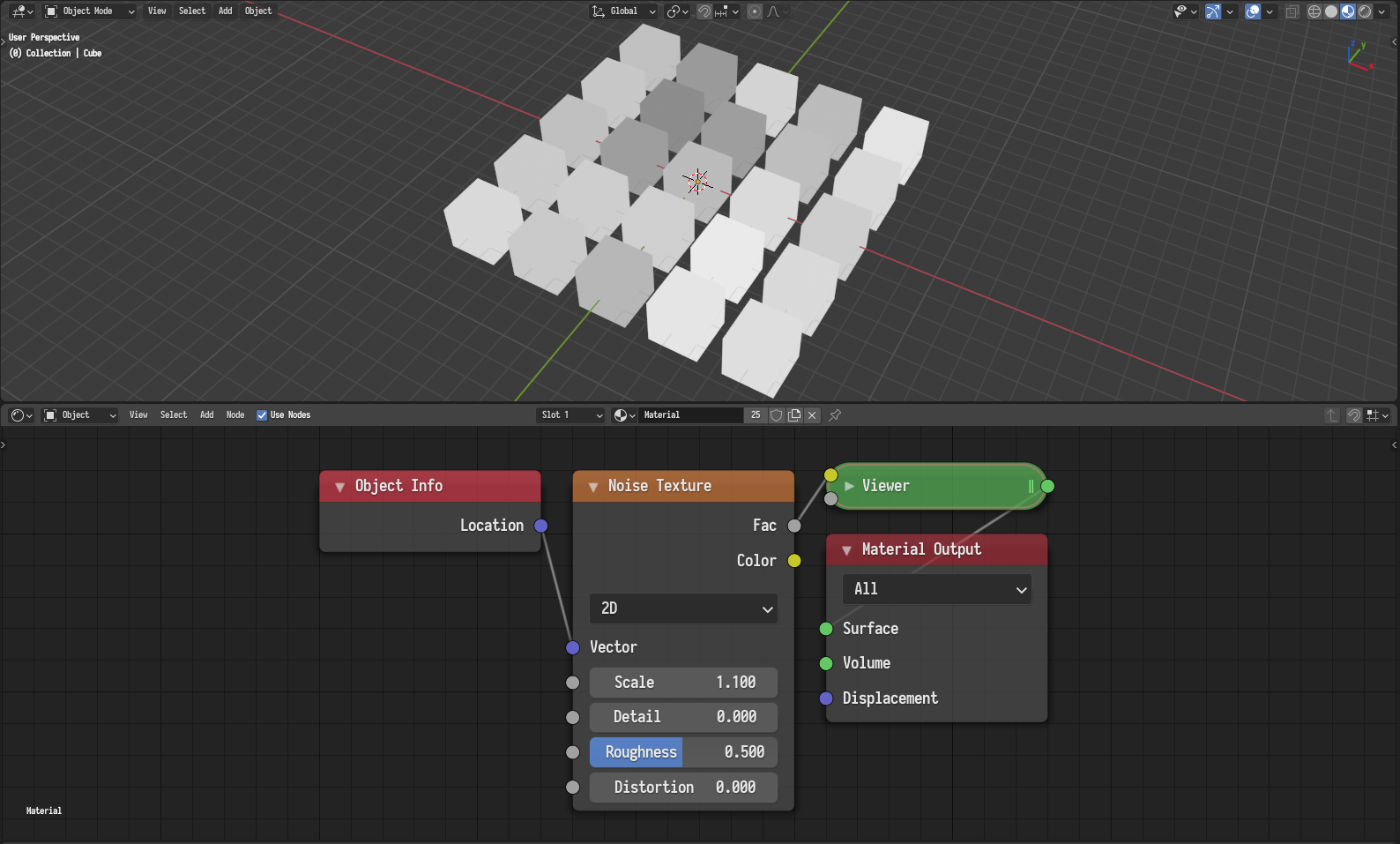
Mitigating the issue by adjusting the scale.# |
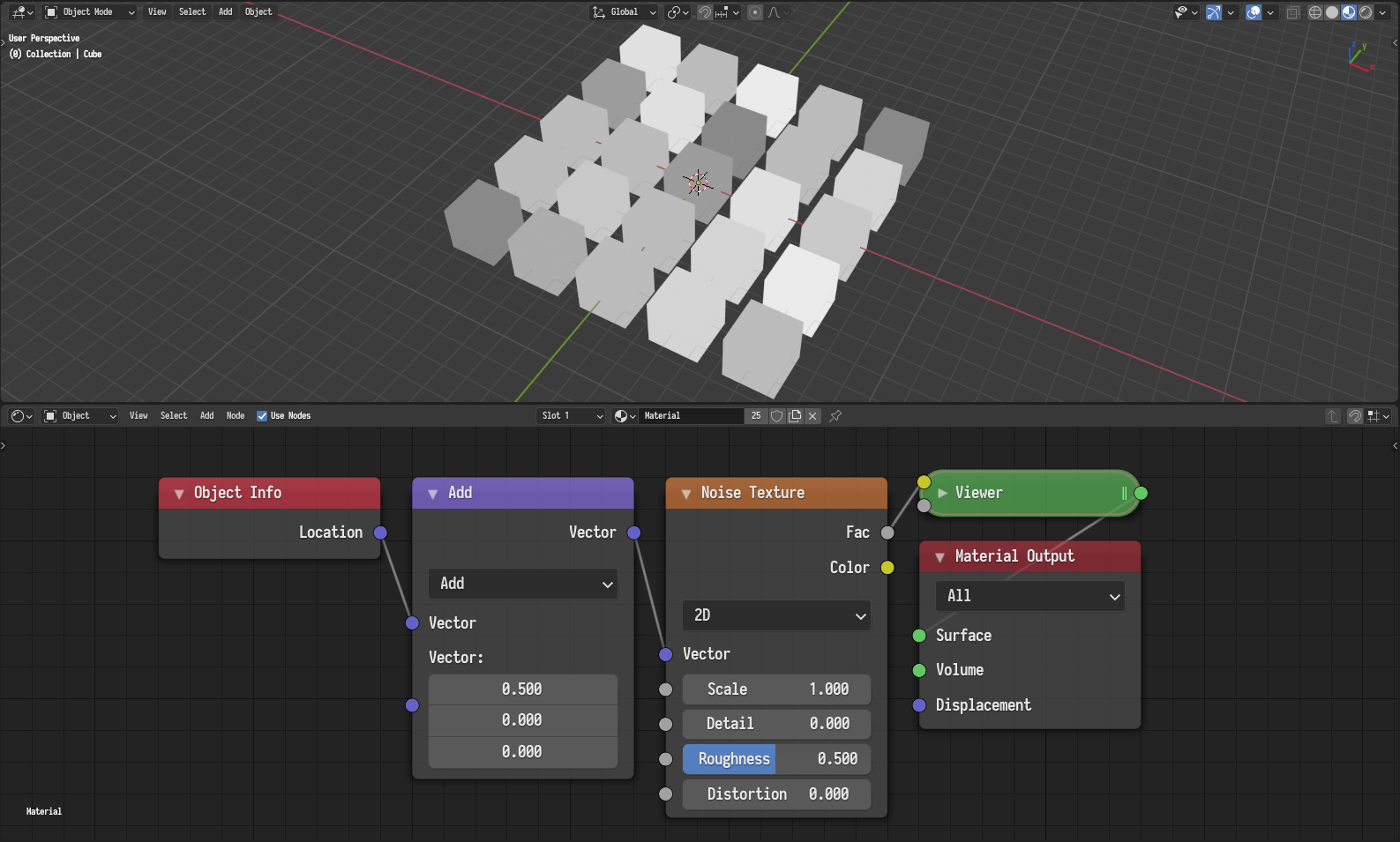
Mitigating the issue by adding an arbitrary offset.# |
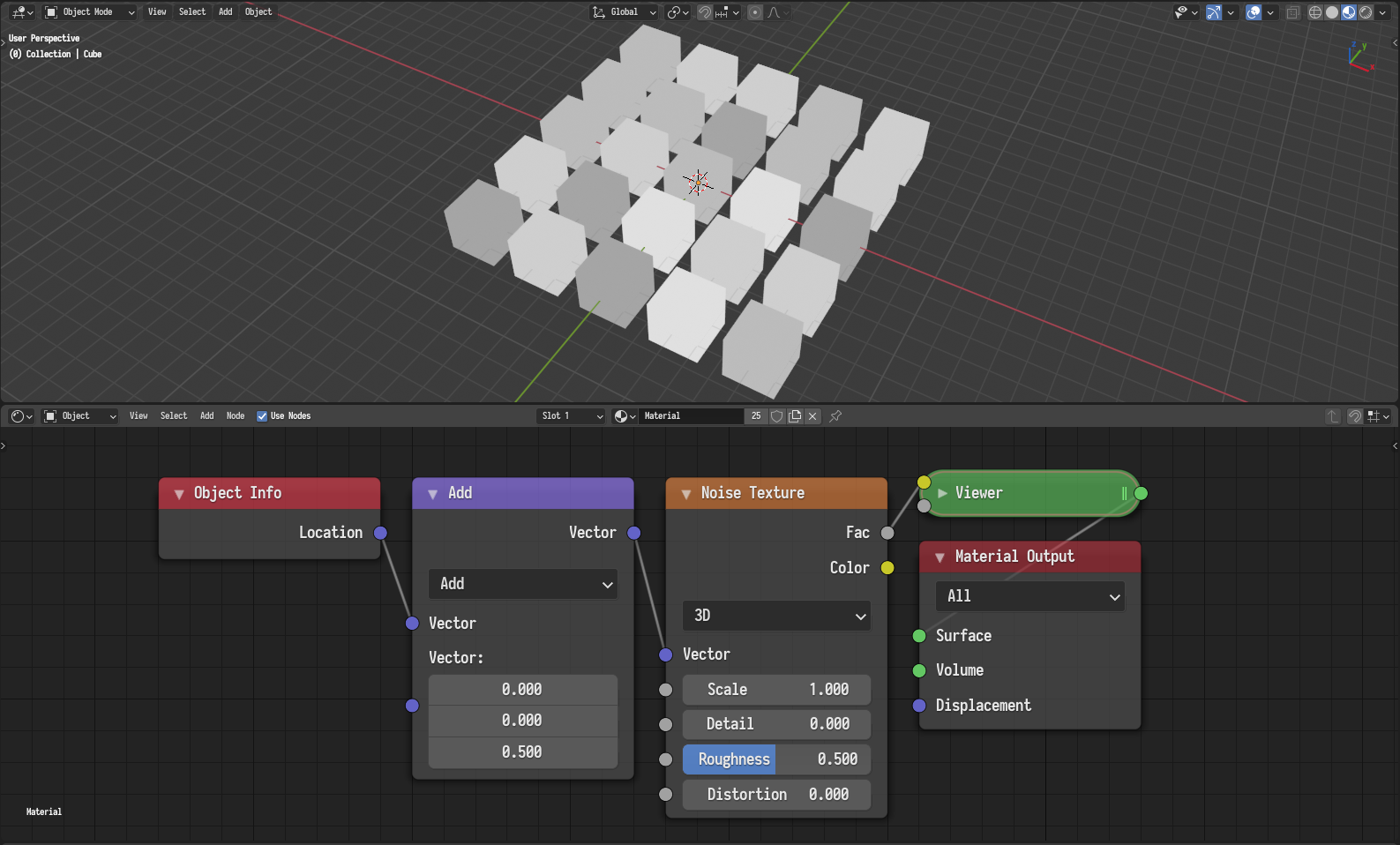
Mitigating the issue by evaluating at a higher dimension.# |
Similarly, in other configurations, one might experience some banding patterns in the noise, where there are bands of high contrast areas followed by banding of low contrast areas. For instance, planar surfaces that are slightly tilted along one of the axis will have such a banding pattern.
An example configuration where the noise have a banding pattern.#
This happens because the slight tilt along one of the axis causes values along the perpendicular axis to change very slowly making the grid structure of the noise more apparent. The easiest way to mitigate this issue to rotate the coordinates by an arbitrary amount.
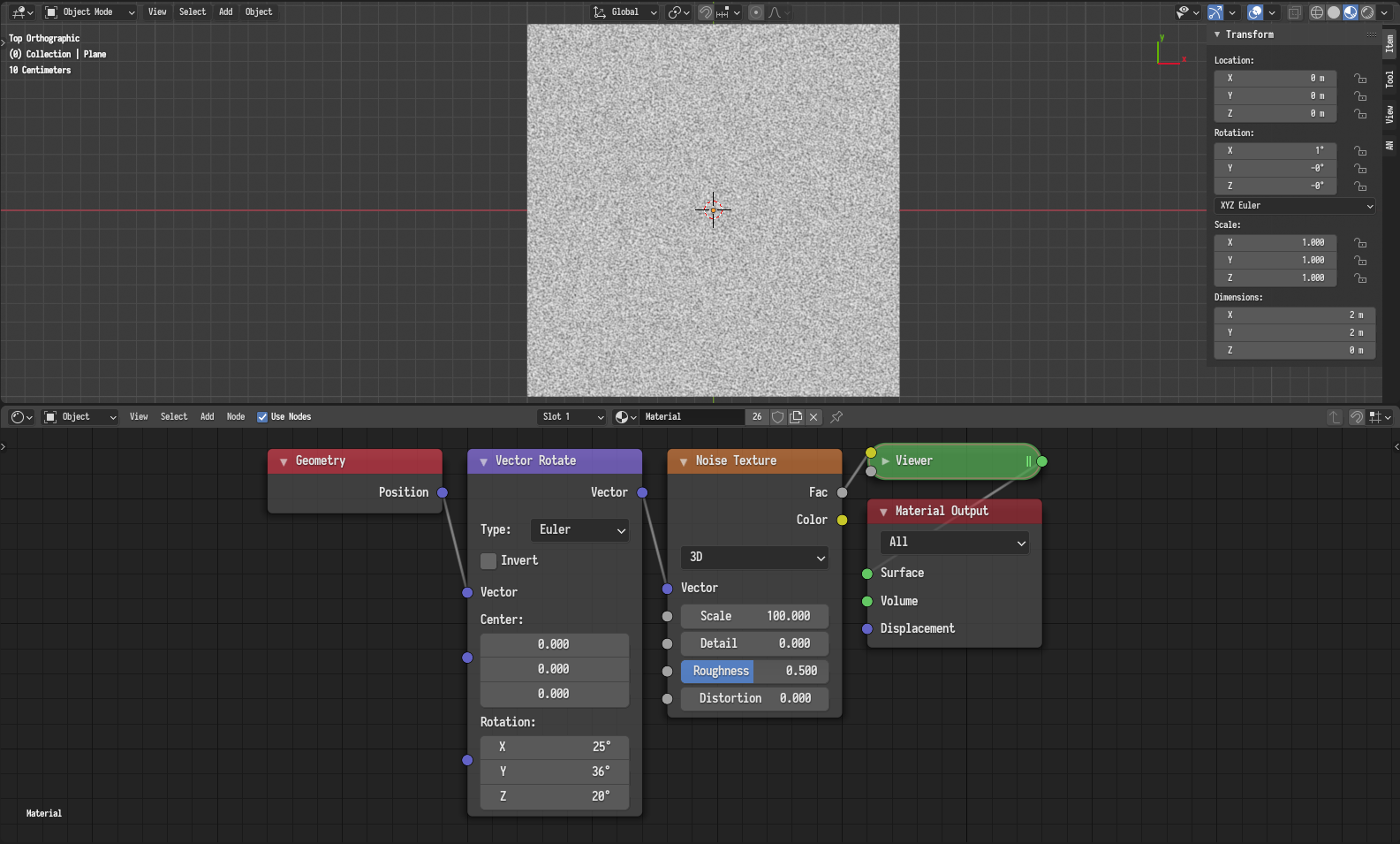
Mitigating the issue by rotating the coordinates by an arbitrary amount.#