Sidebar(サイドバー)¶
Mask Settings¶
- Start Frame, End Frame
Set the frame range of the mask for Sequencer.
Mask Layers¶
Mask Layer panel.¶
Mask layers consists of one or several splines and used to "grouped" operation on splines. Layers can be used to create complex shapes and to define how the splines interact with each other. Splines belonging to the same layer can be animated together, for example by an item from motion tracker footage. Example of such tools might be parenting the whole set of splines to single motion tracking data or simple to transform all of them together.
- Opacity(不透明度)
Used to set the opacity of the mask layer.
- Invert (black/white icon)
Inverts the values (colors) in the mask layer.
- Blend (混合度)
The layer blending operation to perform. See Color Blend Modes.
Modes Merge Add and Merge Subtract give better results when using a Feather on overlapping masks than straightforward mathematical addition and subtraction.
- Falloff(減衰)
Type of the Feather falloff, controls the shape of the transition between black and white.
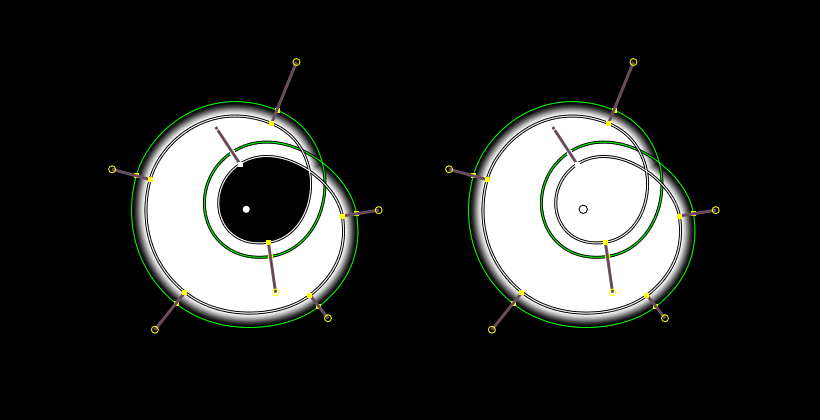
- Overlap
Fills the self-intersecting areas.
- Holes
Overlapping splines from the same layer will generate holes in the mask.
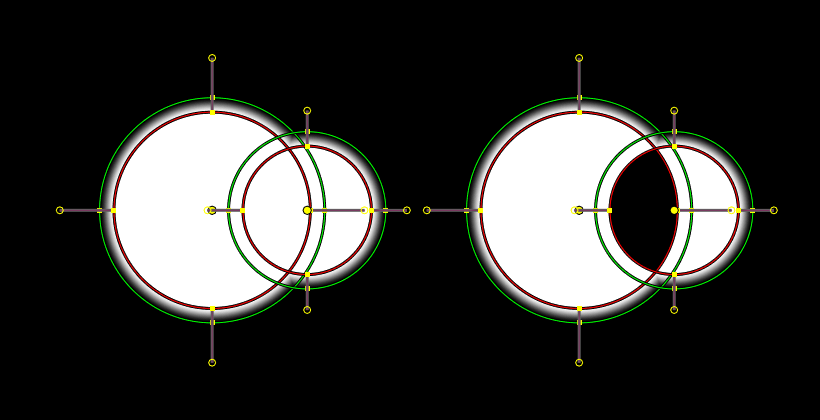
例¶
The purpose of mask layers can be explained with an example. Suppose there are two unwanted people in the footage, and one of them goes from left to right, and the other in the opposite direction. Two mask layers can then be used to mask them separately by using a single mask data-block. At the point of intersection of these shapes they will be added together rather than creating a hole, as would happen if they were on the same layer. If the motion is simple enough, a single motion tracked point can be used to drive the location of the entire mask layer.
Active Spline(アクティブスプライン)¶
Active Spline(アクティブスプライン) パネル。¶
- Feather Offset
The method used for calculating the offset of the mask spline feather.
- Even(均一):
Preserves the thickness of the feather, but can give undesirable loops of the feather curve.
- Smooth(スムーズ):
Gives a nicer and smoother shape, but can also give an undesirable sharp feather when a curve segment forms an S-shape.
- Weight Interpolation
The type of weight (thickness of feather) interpolation between points. Linear or Ease (i.e. changes occur slowly at the beginning and at the end).
- Cyclic(ループ)
If the spline is closed or not.
- Fill(フィル)
Creates splines with filled areas. If disabled, Blender will create curves with a thickness to mask out thin objects such as wires or hair.
- Self Intersection Check
Prevent the feather (not the curve itself) from intersecting with itself.
Active Point¶
Active Point panel.¶
This panel is shown when both a tracking marker and mask is selected.
Parent(親・ペアレント)¶
In the Movie Clip Editor it is possible to link the whole mask or its points to motion tracks. This way the mask or points will follow the tracks.
Animation(アニメーション)¶
Controls animation data for mask properties, including active Actions and their assigned Slot.
See Manually Assigning Actions and Slots for more information.