Armature(アーマチュア)モディファイアー¶
Armature(アーマチュア) モディファイアーは、キャラクターのポーズやポーズをとる必要のあるその他のものをアニメーションするための骨格システム(リグ)を構築するために使用されます。
アーマチュアシステムをオブジェクトに追加することにより、そのオブジェクトを正確に変形できるため、ジオメトリを手動でアニメーション化する必要がありません。
参考
アーマチュアの使用法の詳細については、 アーマチュアのセクション を参照してください。
Options(オプション)¶
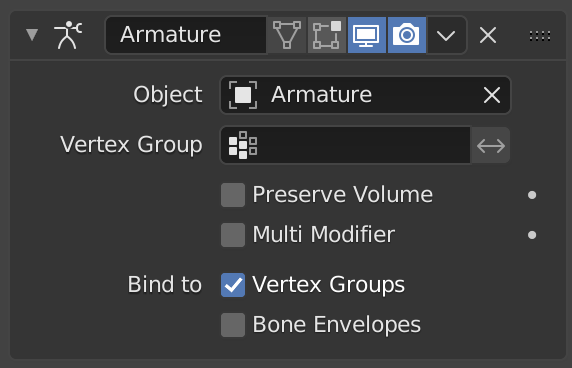
Armature(アーマチュア)モディファイアー。¶
- Object(オブジェクト)
このモディファイアーで使用されるアーマチュアオブジェクトの名前。
- Vertex Group(頂点グループ)
オブジェクトの頂点グループ。このウェイトは、他の アーマチュア の結果と混合するときに、このモディファイアーの結果の影響を判断するために使用されます。
Multi Modifier(マルチモディファイアー) がアクティブになっている状態で、同じオブジェクトにこれらのモディファイアーが少なくとも2つある場合にのみ意味があります。
- Invert
前の設定で定義された頂点グループによって設定された影響を反転します(つまり、このグループのウェイト値を反転します)。
- Preserve Volume(体積を維持)
変形中にオブジェクトのボリュームを維持するためにクォータニオンを使用します。多くの状況でより良い場合があります。
これが無効の場合、ジョイントでの回転は隣接するジオメトリを縮小する傾向があり、静止位置から180度でほぼゼロになります。これが有効の場合、ジオメトリは縮小されなくなりますが、静止位置から180度に達すると不連続になる "ギャップ" があります。
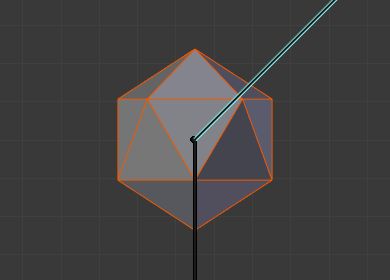
初期状態。¶ |
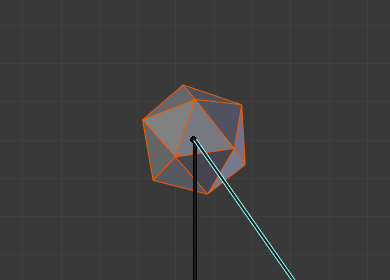
100°回転、 Preserve Volume(体積を維持) は無効。¶ |

180°回転、 Preserve Volume(体積を維持) は無効。¶ |
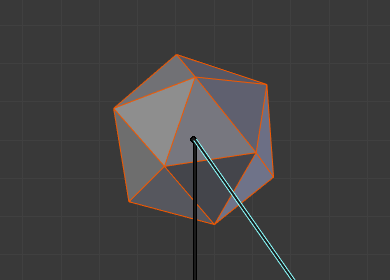
100°回転、 Preserve Volume(体積を維持) は有効。¶ |
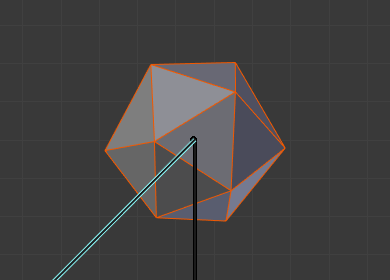
179.9°回転、 Preserve Volume(体積を維持) は有効。¶ |
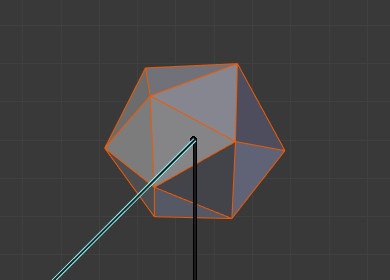
180.1°回転、 Preserve Volume(体積を維持) は有効。¶ |
- Multi Modifier(マルチモディファイアー)
前のモディファイアー(通常は Armature(アーマチュア) モディファイアー)と同じデータを入力として使用します。これにより、複数のアーマチュアを使用して同じオブジェクトを変形できます。これらはすべて "変形されていない" データに基づいています(つまり、2番目の Armature(アーマチュア) モディファイアーが最初のアーマチュアモディファイアーの結果を変形することを回避します...)。
次に、 Armature(アーマチュア) モディファイアー の結果は、 Vertex Group(頂点グループ) のウェイトを "ミキシングガイド" として使用して混合されます。
Tip
Armature(アーマチュア) モディファイアーは、オブジェクトをアーマチュアに 親子化 することにより、オブジェクトにすばやく追加できます。
- Bind to(バインド先)
アーマチュアをメッシュにバインドする方法。
- Vertex Groups(頂点グループ)
メッシュとラティスのみ。有効にすると、指定された名前のボーンは、同じ名前の 頂点グループ に属する頂点を変形します。例えば、 "forearm" という名前のボーンは、 "forearm" 頂点グループの頂点にのみ影響します。
特定の頂点にある1つのボーンの影響は、関連するグループ内のこの頂点のウェイトによって制御されます。 Bone Envelopes(ボーンエンベロープ) よりもはるかに正確な方法ですが、一般的にセットアップに時間がかかります。
- Bone Envelopes(ボーンエンベロープ)
有効にすると、ボーンは、各ボーンのエンベロープ半径と距離によって定義される、頂点またはその近くの制御点を変形します。これにより、 ボーンエンベロープ が変形を制御できるようになります(つまり、ボーンはその近傍の頂点を変形します)。
スキニング方法の例。¶ 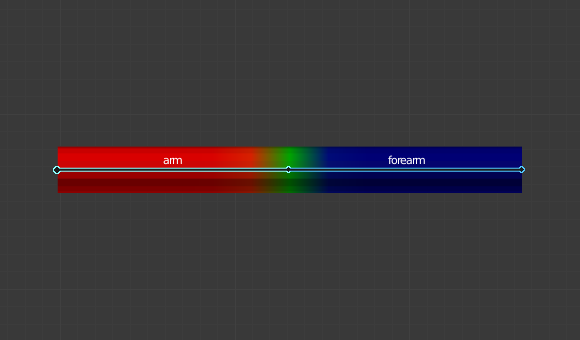
頂点グループ "arm" のウェイト。¶
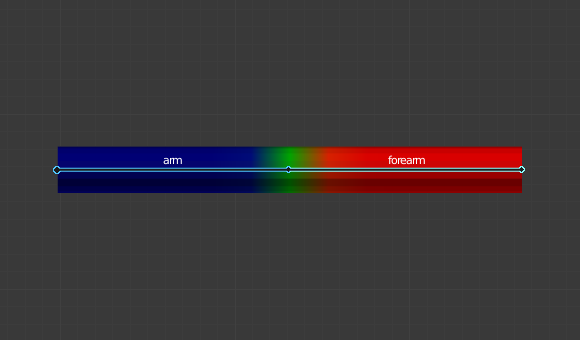
頂点グループ "forearm" のウェイト。¶

アーマチュアをポーズした結果。¶
同じポーズで、頂点グループではなくエンベロープ方法を使用。¶
Tip
エンベロープが無効になっている場合、Blenderは既存の頂点グループ名のセットを使用して、モディファイアーを評価するために実際に必要なボーンを決定します。空の頂点グループを削除すると、依存関係を減らすのに役立ちます。メッシュが同じアーマチュア内の他のボーンの評価中に使用される場合、例えば、 Shrinkwrap(シュリンクラップ) コンストレイントのターゲットとして使用される場合に重要です。