Нода «Рёбра вершины» (edges of vertex node)#
Выбирает соседнее ребро вершины и выводит его индекс.
Эта нода немного особенная, так как она работает в двух разных доменах. Во-первых, она оценивает «вес» для каждого ребра геометрии. Затем, для каждого элемента в контекстном домене, она будет:
Выбирать вершину из геометрии на основе «индекса вершины».
Находить рёбра, соединённые с этой вершиной.
Сортировать эти рёбра по их весу.
Выбирать ребро из отсортированного выше списка на основе «индекса сортировки», где 0 означает ребро с самым меленьким весом, 1 означает ребро с весом чуть побольше и т. д..
Выводить индекс геометрической области этого ребра.
Входы (inputs)#
- Индекс вершины (vertex index)
Индекс вершины, для которой нужно найти рёбра.
Примечание
Если этот вход не подключён, он использует индекс элемента контекста, что означает, что важно, чтобы нода оценивалась в домене «точек».
- Веса (weights)
Веса рёбер геометрии. В отличие от других входов, которые следуют контекстному домену, этот всегда оценивается в домене «рёбер».
Рёбра сортируются по соответствующему весу в порядке возрастания. Рёбра с одинаковым весом сортируются по индексу.
- Индекс сортировки (sort index)
Индекс ребра, начинающийся с 0, для выбора из отсортированных рёбер вершины. Если это значение выходит за пределы диапазона допустимых индексов, оно переносится.
Свойства (properties)#
Эта нода не содержит свойств.
Выходы (outputs)#
- Индекс ребра (edge index)
Индекс геометрической области выделенного ребра. Вы можете передать его в ноду Evaluate at Index или ноду Sample Index (с доменом, установленным на «ребро»), чтобы получить сведения о ребре.
Если вершина не имеет соединённых рёбер, «индекс ребра» будет равен нулю.
- По общему количеству (total)
Количество рёбер, соединённых с выделенной вершиной.
Пример#
В приведённом ниже примере создаётся конус в каждой вершине «куба», выровненный по соседнему ребру, которое является наиболее вертикальным.
Сначала мы делаем «оценку вертикальности» для каждого из рёбер куба. Для этого мы вычитаем положения его вершин, чтобы получить его вектор направления, который мы нормализуем и используем для вычисления скалярного произведения с осью Z. Абсолютное значение этого даёт нам число от 0 до 1, где 0 означает полностью горизонтально, а 1 означает полностью вертикально.
Поскольку рёбра будут сортироваться по возрастанию веса, мы устанавливаем вес = 1 - вертикальность. Таким образом, наиболее вертикально соединённое ребро каждой вершины будет иметь наименьший вес и окажется первым в списке.
Далее, в домене «точек» нам нужно вычислить вращение каждого конуса. С использованием ноды Align Rotation to Vector, задача упрощается, и нам нужно только вычислить вектор направления.
Вектор направления каждого конуса – это центральная точка самого вертикального соседнего ребра за вычетом положения вершины. Нахождение самого вертикального соседнего ребра – это то, где появляется нода Edges of Vertex: для каждой вершины она сортирует соединённые рёбра по их весу и выбирает первое (потому что индекс сортировки равен 0). Как только у нас есть индекс ребра, мы используем ноду Evaluate at Index для получения его центральной точки.
Рассчитав вращения конусов, мы используем ноду Instance on Points для их создания.
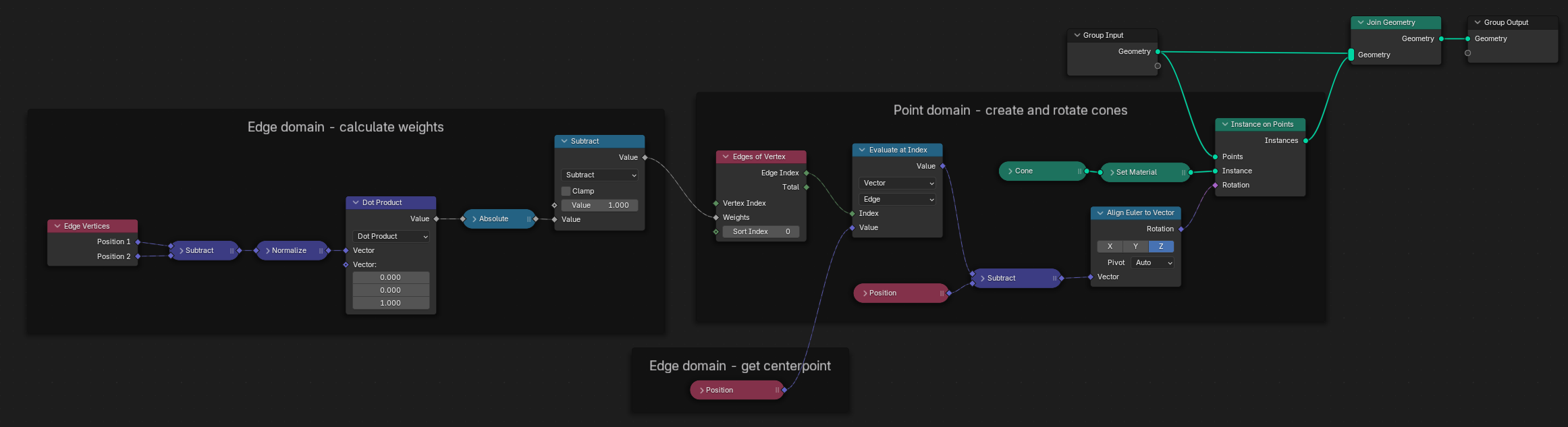
Пример связки нод. (Щёлкните правой кнопкой мышки и выберите «открыть изображение в новой вкладке», чтобы увидеть увеличенную версию.)#
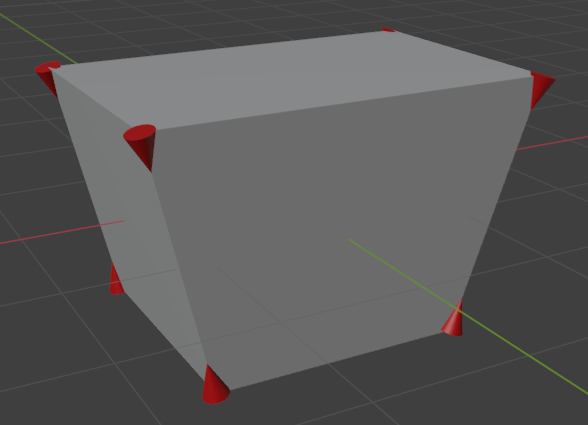
Полученная геометрия.#