Nút Các Cạnh của Điểm Đỉnh (Edges of Vertex Node)

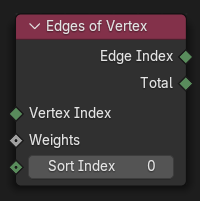
Selects a neighboring edge of a vertex and outputs its index.

This node is a bit special because it operates in two different domains. First, it evaluates a Weight for each edge in the geometry. Then, for each item in the context domain, it will:

• Pick a vertex from the geometry based on the Vertex Index.

• Lùng Tìm the cạnh kết nối tới this điểm đỉnh.

• Sort these edges by their associated weight.

• Pick an edge from the above sorted list based on the Sort Index, where 0 means the edge with the lowest weight, 1 means the edge with the second-lowest weight and so on.

• Đầu Ra the hình học-wide chỉ số của cạnh này.

Đầu Vào (Inputs)

Chỉ Số Điểm Đỉnh (Vertex Index)

The chỉ số của điểm đỉnh cho/đối với which tới lùng tìm the cạnh.

Ghi chú

Nếu this đầu vào được không/không phải/nghịch/phủ định (not) kết nối, it uses the chỉ số (index) của ngữ cảnh phần tử, which means it's quan trọng that the nút tính toán trong Điểm/Chấm phạm vi.

Trọng Lượng (Weights)

The weights of the edges in the geometry. Unlike the other inputs which follow the context domain, this one is always evaluated in the Edge domain.

The edges are sorted by their associated weight in ascending order. Edges with the same weight are sorted by their index.

Chỉ Số Sắp Xếp (Sort Index)

The 0-based index of the edge to select from the vertex's sorted edges. If this value is outside the range of valid indices, it wraps around.

Tính Chất (Properties)

Nút này không có tính chất nào cả.

Đầu Ra (Outputs)

Chỉ Số Cạnh (Edge Index)

The Hình Học-wide Chỉ Số của đã Chọn Cạnh. You có thể Lượt this tới the Tính Toán tại Chỉ Số [Evaluate at Index Node] hoặc the Nút Chỉ Số Mẫu Vật (Sample Index Node) (với the Phạm Vi Đặt tới Cạnh) tới retrieve chi tiết giới thiệu the cạnh.

If the vertex has no connected edges, Edge Index will be zero.

Tổng Số (Total)

The số/lượng của cạnh kết nối tới the đã chọn điểm đỉnh.

Ví Dụ (Example)

The example below creates a cone at each vertex of a "cube," aligned to the neighboring edge that's the most vertical.

First, we calculate a "verticality score" for each of the cube's edges. To do this, we subtract the positions of its vertices to get its direction vector, which we normalize and use to calculate the dot product with the Z axis. The absolute value of that gives us a number between 0 and 1, where 0 means fully horizontal and 1 means fully vertical.

Because the edges will be sorted by ascending weight, we set weight = 1 - verticality. This way, the most vertical connected edge of each vertex will have the lowest weight and come first in the list.

Next, in the point domain, we need to calculate the rotation of each cone. By using the Căn Chỉnh Xoay Chiều theo Véctơ [Align Rotation to Vector Node], the problem gets simplified and we only need to calculate a direction vector.

The direction vector of each cone is the centerpoint of the most vertical neighboring edge minus the position of the vertex. Finding that most vertical neighboring edge is where the Edges of Vertex node comes in: for each vertex, it sorts the connected edges by their weight and pick the first one (because the Sort Index is 0). Once we have the edge's index, we use the Tính Toán tại Chỉ Số [Evaluate at Index Node] to retrieve its centerpoint.

Với the sự xoay chiều của cones tính toán, we sử dụng the Nút Thực Thể Hóa trên Điểm (Instance on Points Node) tới kiến tạo them.

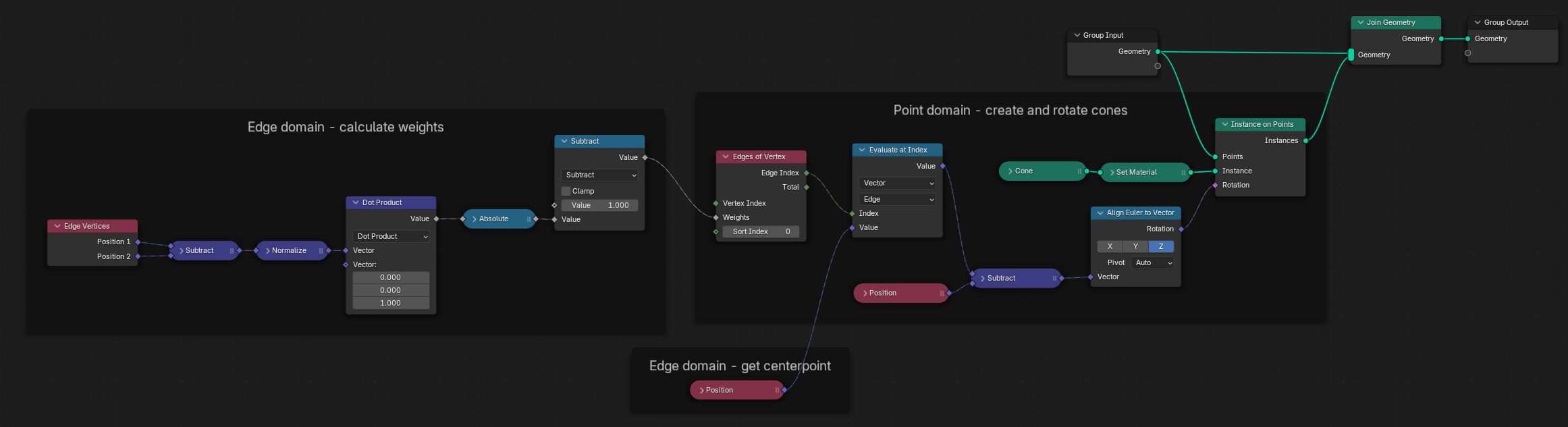
Example node setup. (Right-click and choose "Open image in new tab" to see a larger version.)

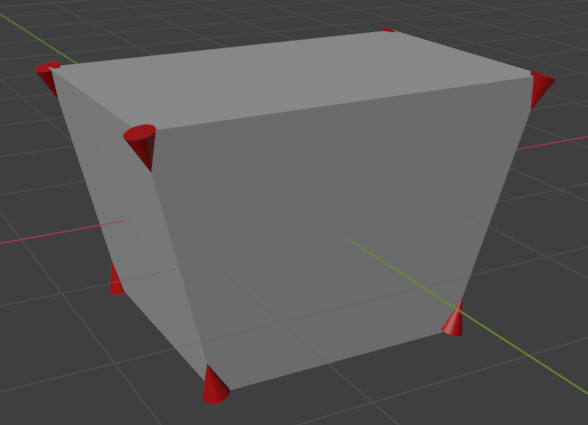
The resulting hình học.