Cấu Trúc (Structure)

Với khung lưới, mọi thứ được xây dựng từ ba cấu trúc cơ bản: "điểm đỉnh", "cạnh" và "các mặt".

../../_images/modeling_meshes_structure_example.svg

Ví dụ về cấu trúc khung lưới.

Vertices (Điểm Đỉnh)

Phần cơ bản nhất của khung lưới là điểm đỉnh (số nhiều trong tiếng Anh là vertices) là một điểm hoặc vị trí đơn lẻ trong không gian 3D. Các điểm đỉnh được đại diện trong Cổng Nhìn 3D ở Chế Độ Biên Soạn dưới dạng các chấm nhỏ. Các điểm đỉnh của một đối tượng được lưu trữ dưới dạng một mảng các tọa độ.

Mẹo

Chớ nhầm tọa độ gốc của đối tượng (object origin) là một điểm đỉnh. Nó có thể trông tương tự, nhưng tọa độ gốc lớn hơn và không thể chọn được.

../../_images/modeling_meshes_structure_cube-example.png

Điểm đỉnh được đánh dấu là "A"; tọa độ gốc của đối tượng được gắn nhãn là "B".

Cạnh (Edges)

Một cạnh luôn luôn nối hai điểm đỉnh bằng một đường thẳng. Các cạnh là "đường dây" mà bạn nhìn thấy khi quan sát khung lưới trong góc nhìn khung dây. Chúng thường không xuất hiện trên hình ảnh kết xuất. Chúng được sử dụng để xây dựng các mặt.

Các Mặt (Faces)

Mặt được sử dụng để xây dựng Mặt thực của đối tượng. Chúng là những gì bạn thấy khi kết xuất khung lưới. Nếu khu vực này không chứa một mặt thì nó sẽ đơn giản là trong suốt hoặc không tồn tại trong hình ảnh kết xuất.

Một mặt được định nghĩa là diện tích giữa ba (tam giác), bốn (tứ giác) hoặc nhiều hơn (n-gons) điểm đỉnh, với một cạnh ở mỗi bên. Các mặt thường được viết tắt thành "tam giác, tứ giác và đa giác".

Hình tam giác luôn luôn bằng phẳng và do đó dễ tính toán. Mặt khác, tứ giác "biến dạng dễ dàng" và do đó được sử dụng nhiều cho hoạt họa và phân hóa mô hình.

Xem thêm

Pháp Tuyến (Normals)

Trong hình học, pháp tuyến là một hướng hoặc đường vuông góc với một cái gì đó, điển hình là một hình tam giác hoặc một bề mặt, song cũng có thể tương đối với một đường thẳng, một đường tiếp tuyến cho một điểm trên một đường cong, hoặc một bình diện tiếp tuyến cho một điểm trên một bề mặt.

Normals help to determine the shading of the mesh among other things.

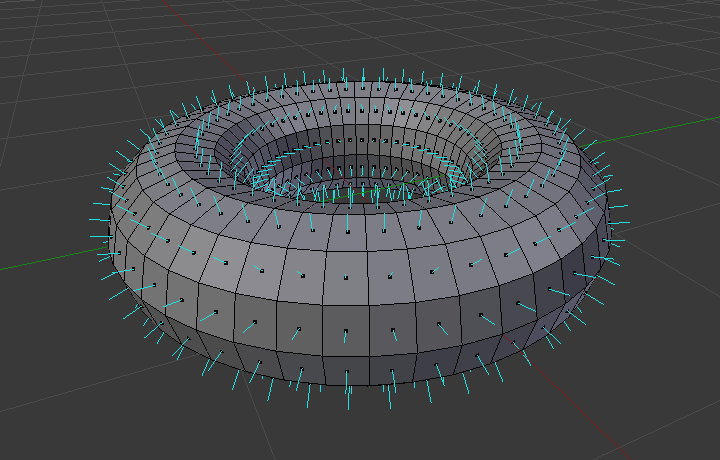
../../_images/modeling_meshes_structure_viewport.png

Một diễn họa trực quan về các pháp tuyến mặt của một hình xuyến.

Trong hình trên, mỗi đường màu xanh lam đại diện cho pháp tuyến của một mặt trên hình xuyến. Các đường thẳng vuông góc với mặt mà chúng nằm trên đó. Sự hình dung trực quan có thể được kích hoạt, trong Chế Độ Biên Soạn, trong Bảng Vẽ Lồng Khung Lưới của Cổng Nhìn (Mesh Display Viewport Overlays panel).

Shading (Tô Bóng)

Surface normals play a fundamental role in determining how light interacts with 3D objects and thus greatly influence the shading of those objects. Normals can be shaded smooth or flat.

When a mesh uses flat shading, the faces are rendered and displayed faces uniformly. This is usually desirable for objects with flat surfaces such as a cube or pyramid.

When a mesh uses smooth shading, the normals are interpolated across the vertices of a polygonal mesh, smooth transitions between adjacent polygons can be achieved, resulting in a more realistic appearance.

By default face normals have flat shading however, this can be adjusted either for the whole object or per face.

To adjust the shading of the whole object, use:

To revert to flat shading, use Tô Bóng Phẳng (Shade Flat).

The shading of objects can also be adjusted per face, edge, or vertex.

Pháp Tuyến Tách Phân Tùy Chỉnh (Custom Split Normals)

"Pháp Tuyến Tách Phân Tùy Chỉnh" là một phương pháp để điều chỉnh/tô bóng giả bằng cách hướng các pháp tuyến theo chiều hướng khác với các pháp tuyến mặc định, và được tính toán tự động. Nó chủ yếu được sử dụng trong phát triển trò chơi, nơi nó giúp giải quyết một số vấn đề do các đối tượng có độ đa giác thấp tạo ra (ví dụ phổ biến nhất là cấu trúc cây có số đa giác thấp, bụi rậm, cỏ, v.v. và các góc 'tròn').

Blender hỗ trợ định mức tùy chỉnh trên cơ sở 'phân hình quạt mềm mại'kết nối''kết nối' bằng các cạnh mịn màng. Chức năng này có nghĩa là bạn có thể có các pháp tuyến trên mỗi góc mặt, trên một tập hợp các góc mặt kề cận hoặc trên mỗi điểm đỉnh.

Mẹo

The computation of Custom Split Normals can be disabled to improve performance. This option can be found in the Simplify Rendering Settings.

Biên Soạn các Pháp Tuyến Tách Phân Tùy Chỉnh (Editing Custom Split Normals)

Tham Chiếu (Reference)

Chế Độ (Mode):

Chế Độ Biên Soạn (Edit Mode)

Trình Đơn (Menu):

Khung Lưới (Mesh) ‣ Pháp Tuyến (Normals)

Tổ Hợp Phím Tắt (Shortcut):

Alt-N

Có một số công cụ dành cho việc biên soạn các pháp tuyến tách phân tùy chỉnh. Các công cụ biên soạn khung lưới pháp tuyến tùy chỉnh có thể ảnh hưởng đến toàn bộ các pháp tuyến (mặc định), hoặc chỉ những cái được chọn mà thôi. Để chọn một pháp tuyến tùy chỉnh liên quan với một điểm đỉnh và mặt nào đó:

  • Thực hiện chế độ chọn phần tử cả Điểm Đỉnh và Mặt (sử dụng Shift-NCT (LMB) để bật chế độ thứ hai).

  • Chọn một hoặc nhiều điểm đỉnh, sau đó chọn một mặt. Chức năng này có thể được lặp lại để chọn nhiều điểm đỉnh hơn và một mặt khác v.v. Chúng ta có thể dễ dàng nhận thấy tác dụng của các công cụ này nếu chúng ta bật tùy chọn "Vẽ pháp tuyến của điểm đỉnh trên mỗi mặt như các đường thẳng" trong Lớp Vẽ Lồng Chế Độ Biên Soạn .

Xem thêm

Biên Soạn Pháp Tuyến (Editing Normals).

Nhập Khẩu các Pháp Tuyến Tách Phân Tùy Chỉnh (Importing Custom Split Normals)

Một số công cụ, đặc biệt là những công cụ được sử dụng trong CAD, có xu hướng tạo ra hình học bất thường khi phân hóa các đối tượng thành các khung lưới (hình tam giác rất mỏng và dài, v.v.). Các pháp được tuyến tính toán tự động trên các hình học như vậy thường tạo ra các giả tượng xấu, do đó, điều quan trọng là phải có khả năng nhập khẩu và sử dụng các pháp tuyến do chính bản thân công cụ CAD tạo ra.

Ghi chú

Hiện tại, chỉ có Trình Nhập Khẩu FBX (FBX Importer) và Trình Nhập Khẩu Alembic (Alembic Importer) là có khả năng nhập khẩu các pháp tuyến tùy chỉnh mà thôi.

Topology (Cấu Trúc Liên Kết)

Vòng Mạch (Loops)

../../_images/modeling_meshes_structure_edge-face-loops.png

Các vòng cạnh và vòng mặt.

Các vòng "Cạnh" và "vòng mạch" là tập hợp của các mặt hoặc các cạnh tạo thành các "vòng mạch" liên tục như trong hình minh họa Các vòng cạnh và vòng mặt..

Trong hình trên, các vòng mạch không kết thúc ở các cực là các vòng mạch tuần hoàn (1 và 3). Chúng bắt đầu và kết thúc ở cùng một điểm đỉnh và chia mô hình thành hai phân vùng. Vòng mạch có thể là một công cụ nhanh chóng và hữu hiệu để làm việc với các vùng cụ thể, liên tiếp của khung lưới, và là điều kiện tiên quyết cho quá trình hoạt họa nhân vật tự nhiên. Để biết miêu tả chi tiết về phương pháp làm việc với các vòng mạch trong Blender thì xin hãy xem: Chọn các Vòng Cạnh (Select Edge Loops).

Ghi chú

Lưu ý rằng các vòng mạch (2 và 4) không chạy quanh toàn bộ mô hình. Các vòng mạch dừng lại ở cái vốn gọi là cực, bởi vì không có phương pháp đơn nhất nào để tiếp tục một vòng mạch từ một cực cả. Cực là các điểm đỉnh được nối với ba, năm hoặc nhiều cạnh. Do đó, các điểm đỉnh kết nối với chính xác một, hai hoặc bốn cạnh sẽ không phải là cực.

Vòng Cạnh (Edge Loops)

Các vòng (1 và 2) trong hình minh họa Các vòng cạnh và vòng mặt. là các vòng cạnh. Chúng kết nối các điểm đỉnh, hầu cho mỗi điểm đỉnh trên vòng mạch có đúng hai hàng xóm không nằm trong vòng mạch, và được đặt ở hai bên của vòng mạch (ngoại trừ điểm đỉnh đầu và cuối trong trường hợp các cực).

Vòng cạnh là một khái niệm quan trọng, đặc biệt là trong quá trình tạo mô hình hữu cơ (dưới bề mặt) và hoạt họa nhân vật. Khi được sử dụng đúng cách, chúng cho phép bạn xây dựng các mô hình với tương đối ít số điểm đỉnh song trông rất tự nhiên khi được sử dụng như các bề mặt phân hóa và biến dạng rất tốt trong hoạt họa.

Lấy hình minh họa Các vòng cạnh và vòng mặt. trong mô hình hữu cơ làm ví dụ, các vòng cạnh đi theo các đường viền và đường biến dạng tự nhiên của da và các cơ bắp bên dưới. Các vòng mạch dày đặc hơn ở những khu vực biến dạng nhiều hơn khi nhân vật di chuyển, ví dụ như ở vai hoặc đầu gối.

Bạn có thể tìm thêm thông tin chi tiết về cách làm việc với các vòng cạnh trong Chọn các Vòng Cạnh (Select Edge Loops).

Vòng Mặt (Face Loops)

Đây là một phần mở rộng hợp lý của các vòng cạnh, ở chỗ chúng bao gồm các mặt nằm giữa hai vòng cạnh, như được thể hiện trong các vòng (3 và 4) trong hình minh họa Các vòng cạnh và vòng mặt.. Lưu ý rằng đối với các vòng không tuần hoàn (4), các mặt chứa các cực hội tụ sẽ không được bao gồm trong một vòng mặt.

Bạn có thể tìm thêm thông tin chi tiết về cách làm việc với các vòng Mặt trong Lựa Chọn Vòng mặt (Face Loop Selection).

Các Điểm Cực/Hội Tụ (Poles)

Xin xem mục CỰC-N & Cực-e (N-poles & E-poles).

Phi Đa Tạp (Non-Manifold)

Xin xem mục Non-manifold (Phi đa tạp).