松弛¶
参考
- 模式:
编辑模式
- 工具:
松弛工具可用于更均匀地分布 UV。它的工作原理是沿着 UV 边缘拉动顶点,使 UV 展开达到平衡。
松弛工具可与最小化拉伸工具进行比较,后者可直接作用于面,以减少纹理拉伸和剪切。您可能会发现,有时最小化拉伸效果更好,有时是展开工具,有时是松弛工具。
首先使用展开,然后使用最小化拉伸,再用松弛工具进行修饰,往往能达到最佳效果。请记住,您可以随时使用 “撤销” 来返回到之前的状态。
工具设置¶
- 尺寸
该选项控制笔刷的半径,以像素为单位。F 允许你通过拖动鼠标和 鼠标左键 交互式地改变笔刷大小。在使用 F 时输入一个数字然后回车可以让你更改数字大小。
- 强度
控制笔刷的每次应用对 UV 的影响程度。您可以通过在 3D 视窗中按下 Shift-F,然后移动画笔,再按下 鼠标左键 来交互地改变其强度。您也可以在 Shift-F 调整尺寸时输入数字。
- 衰减
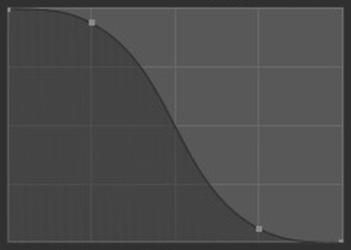
衰减控制笔刷衰减的 强度。衰减从笔刷的中心(曲线的左侧部分)映射到其边界(曲线的右侧部分)。更改曲线的形状将使笔刷更软或更硬。更多信息请查看曲线部件。
- 曲线预设
- 自定义:
你可以通过手动操作曲线部件中的控制点来选择如何确定从笔刷中心到边界的衰减强度。曲线部件的底部也有一些预设的自定义曲线,可以单独使用,也可以作为调整的起点。
- 平滑化:
中心强度、边界强度和它们之间的衰减过渡均匀分布。
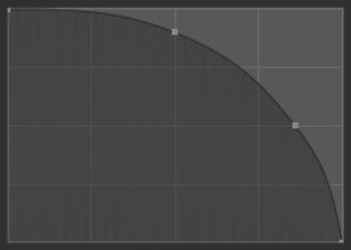
- 更平滑:
类似于 平滑,但在逐渐变细之前产生更宽的笔刷中心点。
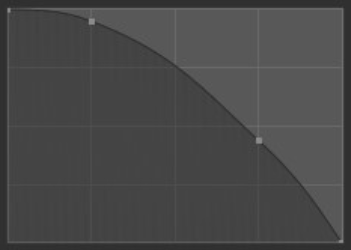
- 球形:
笔刷的强度主要在其最强点,在笔刷边缘附近具有陡峭的衰减。
- 根凸:
类似于球形,但中心是一个更集中的点。
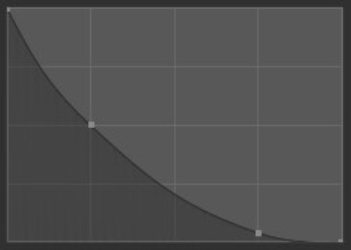
- 锐利:
笔刷的中心是最强的点,然后呈指数级逐渐减小到较低的强度,从而产生一个细点。
- 线性:
由于中心是最强的,因此当它到达笔刷的边界时,强度会不断减弱。
- 更锐利:
与 锐利 类似,但中心点更浓缩。
- 反向平方:
平滑 和 球形 之间的混合体。
- 常量:
整个笔刷的力度保持一致。这将在笔刷边界处形成锐利的边缘。
- 选项
- 锁定边界
锁定 UV 孤岛边界,免受笔刷影响,用于保持 UV 孤岛形状。
- 雕刻所有孤岛
编辑所有孤岛,而不是只编辑开始雕刻时最靠近笔刷中心的孤岛。
- 方法
如何确定边的权重:
- 拉普拉斯:
The classic discrete Laplace operator applied to the UV graph. Each edge has equal weighting, resulting in triangles which resemble a honeycomb shape, or quads aligned into square grid.
- HC:
与拉普拉斯方法类似,HC 方法也使用均等权重,同时努力保持网格密集区域与边较少区域之间的梯度。
Note, this method uses the "Humphrey's Classes" operator as described in the paper: "Improved Laplacian Smoothing of Noisy Surface Meshes".
- 几何数据:
Edges are weighted according to the discrete Laplace operator (cotangent formula) applied to the 3D geometry. This tries to bring the relative lengths of edges in UV closer to the relative lengths of edges in 3D, resulting in a UV unwrap with less distortion across edge boundaries.