Nodo Gabor

El nodo de textura Gabor evaluará un ruido de tipo Gabor en las coordenadas de texturizado de entrada. El ruido de tipo Gabor se caracteriza visualmente por presentar bandas aleatoriamente entrelazadas, cuya dirección y ancho podrán ser controlados. Adicionalmente, podrá ser usado para crear ruidos de tipo omnidireccional, como sucede con el nodo estándar de textura de Ruido, aunque al ser más lento de calcular, probablemente seguirá siendo una mejor opción usar el nodo Ruido en muchos casos. Ver los ejemplos abajo para obtener una mejor noción de sus posibles usos.

Entradas

Vector

Las coordenadas en las que el ruido de tipo Gabor será evaluado. El componente Z será ignorado al usar el tipo de ruido 2D. De forma predefinida el nodo usará las coordenadas de texturizado Generadas, en caso de que esta entrada permaneciera desconectada.

Escala

Escala del ruido de tipo Gabor.

Frecuencia

La frecuencia a la que el ruido Gabor cambiará en el espacio. Se diferenciará de la entrada Escala en que sólo escalará de forma perpendicular a la dirección del ruido.

Anisotropía

La direccionalidad del ruido Gabor. 1 significará que el ruido será completamente direccional, mientras 0 significará que el ruido será omnidireccional.

Orientación

La dirección del ruido anisótropo. Se trata de un ángulo, para el tipo 2D, o un versor de dirección, para el tipo de ruido 3D.

Propiedades

Tipo

El tipo de textura de ruido Gabor.

2D:

Evaluará el ruido en un espacio 2D. El componente Z del vector de entrada será ignorado.

3D:

Evaluará el ruido en un espacio 3D.

Nota

Al aumentar el número de dimensiones aumentará el tiempo de procesamiento, razón por la cual debería usarse la dimensión más baja posible, salvo estricta necesidad.

Salidas

Valor

El valor del ruido de tipo Gabor, con intensidad y fase aleatorias. Será igual al seno de la fase multiplicado por la intensidad.

Fase

La fase del ruido Gabor, sin intensidad aleatoria.

Intensidad

La intensidad del ruido Gabor, sin fase aleatoria.

Ejemplos

La siguiente tabla demuestra diferentes resultados del nodo, usando diferentes parámetros. Como se puede apreciar, el ruido se encuentra caracterizado visualmente por bandas entrelazadas que generalmente estarán orientadas en una dirección específica. Aún así, será posible adjudicar valores menores de 1 al parámetro Anisotropía para crear bandas con direcciones más aleatorias. El parámetro Frecuencia determinará la cantidad de bandas perpendiculares a la dirección del ruido. Sin embargo, el parámetro Escala también podrá ser usado para aumentar globalmente la cantidad de bandas, por lo que sería recomendable comenzar por aumentar primero el parámetro de escala, dado que el ruido de alta frecuencia será más proclive a sufrir de un bajo contraste y un entrelazamiento limitado de las bandas.

Diferentes resultados con distintos parámetros.

Salida de Valor. Frecuencia = 2. Anisotropía = 1.	Salida de Fase. Frecuencia = 2. Anisotropía = 1.	Salida de Intensidad. Frecuencia = 2. Anisotropía = 1.
Salida de Valor. Frecuencia = 3. Anisotropía = 1.	Salida de Fase. Frecuencia = 3. Anisotropía = 1.	Salida de Intensidad. Frecuencia = 3. Anisotropía = 1.
Salida de Valor. Frecuencia = 2. Anisotropía = 0.7.	Salida de Fase. Frecuencia = 2. Anisotropía = 0.7.	Salida de Intensidad. Frecuencia = 2. Anisotropía = 0.7.

El ruido Gabor puede ser descompuesto en componentes de Fase e Intensidad, en donde el valor final del ruido será calculado como el seno de la fase multiplicado por la intensidad; nótese que la fase se encontrará normalizada (en un rango de 0 a 1).

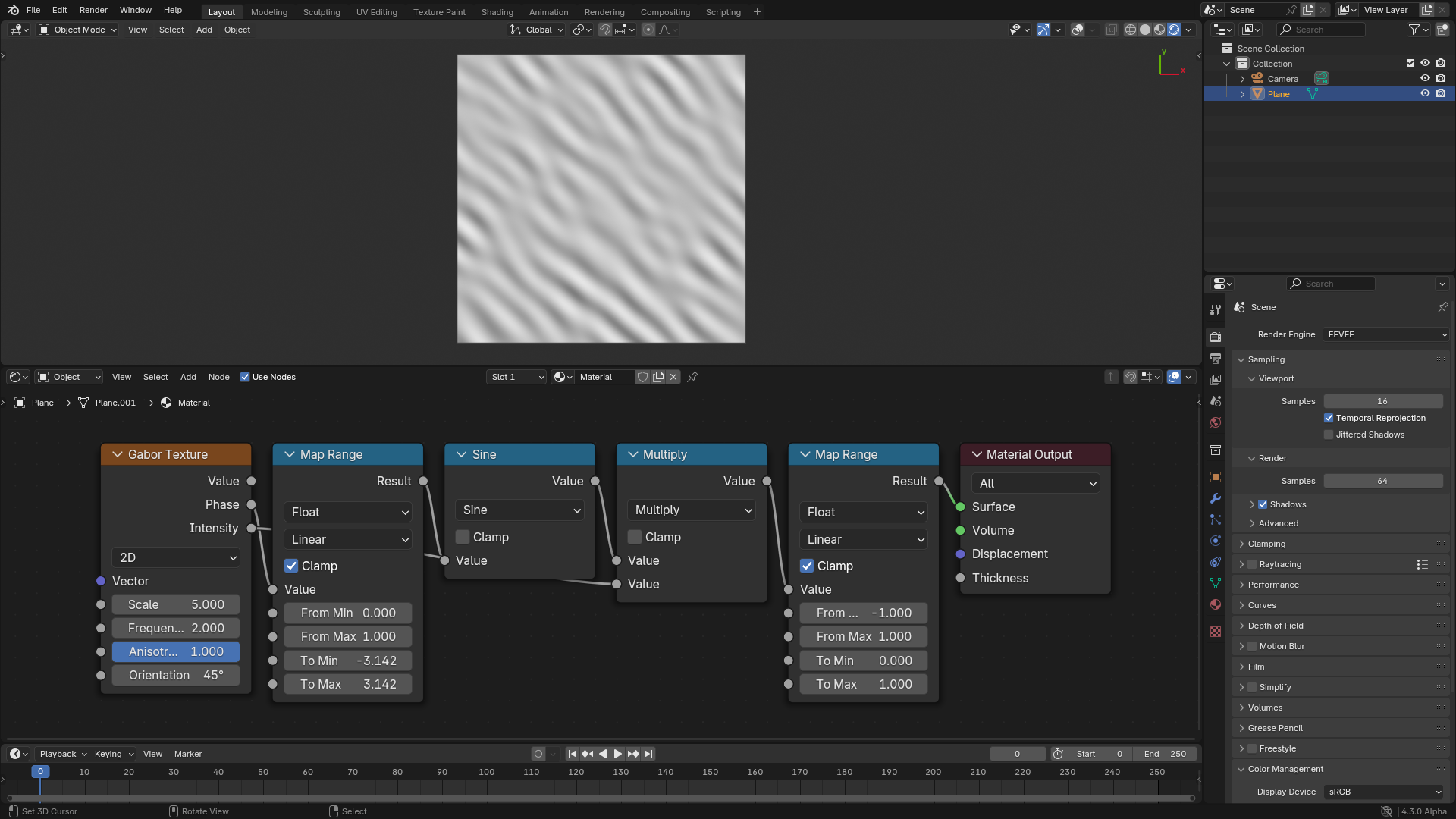
Cálculo del valor final de salida a partir de las salidas de fase e intensidad.

La ventaja de la salida Fase es que no presenta intensidades aleatorias ni áreas de bajo contraste, como sí sucede con la salida de Valor, por lo que podrá ser usada como base para texturas de naturaleza más estructurada, como por ejemplo sería el caso de dunas de arena.

Estructuras de tipo dunas de arena, usando la salida de Fase.

La principal ventaja de la salida de Intensidad es que proporciona información acerca de la ubicación de singularidades en la salida de Fase. Las singularidades son aquellas áreas de la fase en donde las bandas se cruzan (mostradas en rojo en la figura a continuación). Esas áreas tendrán una intensidad cercana a cero en la salida de Intensidad. Por lo que, en caso de que no se deseara ver esas áreas, será posible ocultarlas multiplicándolas por una variante de la salida de Intensidad.

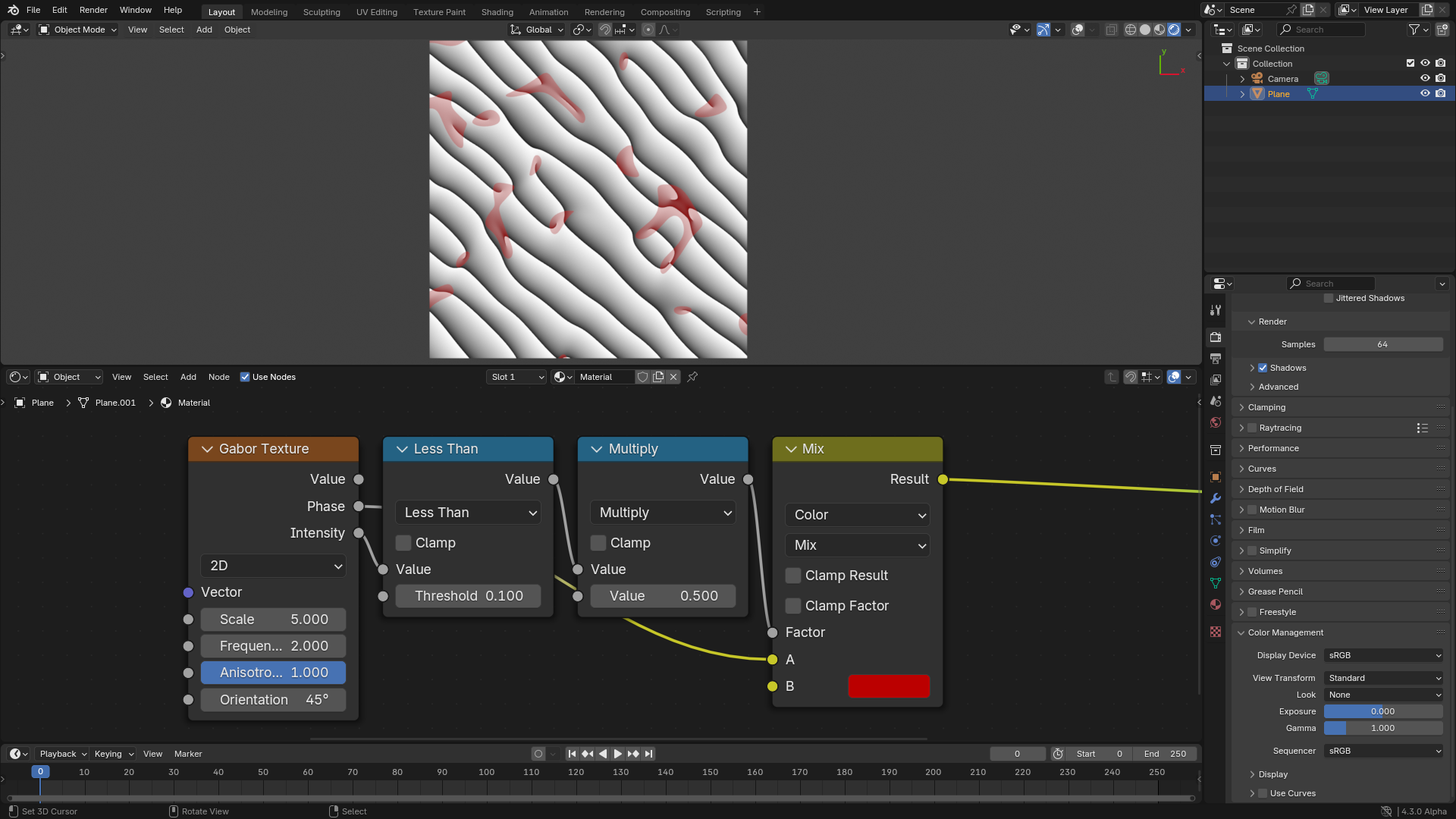
Visualización de las área en donde ocurren singularidades.

Las entradas podrán ser variadas a lo largo del espacio, para producir patrones más interesantes.

Variación de la frecuencia y la orientación a lo largo del espacio.