Nodo Bordes de vértice¶
Selects a neighboring edge of a vertex and outputs its index.
This node is a bit special because it operates in two different domains. First, it evaluates a Weight for each edge in the geometry. Then, for each item in the context domain, it will:
Escogerá un vértice de la geometría basándose en el Identificador de vértice.
Encontrará los bordes conectados a este vértice.
Sort these edges by their associated weight.
Pick an edge from the above sorted list based on the Sort Index, where 0 means the edge with the lowest weight, 1 means the edge with the second-lowest weight and so on.
Devolverá el identificador de este borde a nivel de la geometría.
Entradas¶
- Identificador de vértice
El identificador del vértice para el cual se deberán encontrar los bordes.
Nota
En caso de que esta entrada se encontrara desconectada, usará el identificador del elemento del contexto, lo que significa que será importante que el nodo sea evaluado en el dominio Punto.
- Influencias
The weights of the edges in the geometry. Unlike the other inputs which follow the context domain, this one is always evaluated in the Edge domain.
The edges are sorted by their associated weight in ascending order. Edges with the same weight are sorted by their index.
- Identificador de ordenamiento
El identificador del borde del vértice a ser seleccionado (iniciando en 0). Si este valor se encontrara fuera del rango de identificadores válidos, volverá a iniciar desde 0.
Propiedades¶
Este nodo no contiene propiedades.
Salidas¶
- Identificador de borde
El identificador del borde seleccionado, a nivel de la geometría. Será posible pasarlo al Nodo Evaluar en identificador o el Nodo Muestrear identificador (con su dominio definido en Borde) para obtener detalles acerca del borde.
If the vertex has no connected edges, Edge Index will be zero.
- Total
La cantidad de bordes conectados al vértice seleccionado.
Ejemplo¶
The example below creates a cone at each vertex of a «cube,» aligned to the neighboring edge that’s the most vertical.
First, we calculate a «verticality score» for each of the cube’s edges. To do this, we subtract the positions of its vertices to get its direction vector, which we normalize and use to calculate the dot product with the Z axis. The absolute value of that gives us a number between 0 and 1, where 0 means fully horizontal and 1 means fully vertical.
Because the edges will be sorted by ascending weight, we set weight = 1 - verticality. This way, the most vertical connected edge of each vertex will have the lowest weight and come first in the list.
Next, in the point domain, we need to calculate the rotation of each cone. By using the Nodo Alinear rotación a vector, the problem gets simplified and we only need to calculate a direction vector.
The direction vector of each cone is the centerpoint of the most vertical neighboring edge minus the position of the vertex. Finding that most vertical neighboring edge is where the Edges of Vertex node comes in: for each vertex, it sorts the connected edges by their weight and pick the first one (because the Sort Index is 0). Once we have the edge’s index, we use the Nodo Evaluar en identificador to retrieve its centerpoint.
Con las rotaciones de los conos calculadas, se usará el Nodo Instanciar en puntos para crearlos.
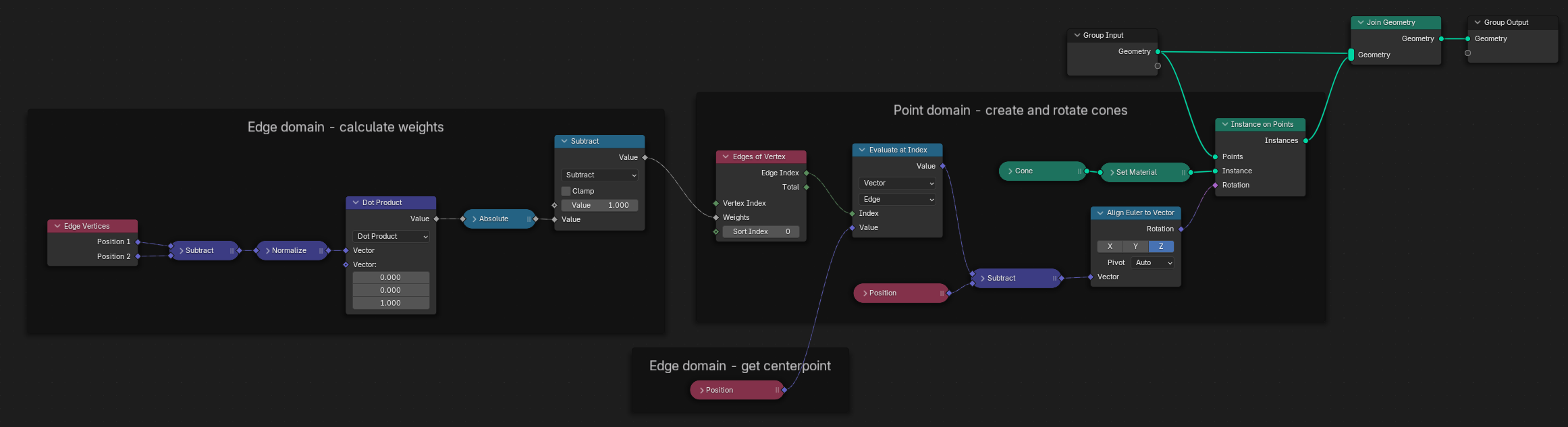
Example node setup. (Right-click and choose «Open image in new tab» to see a larger version.)¶
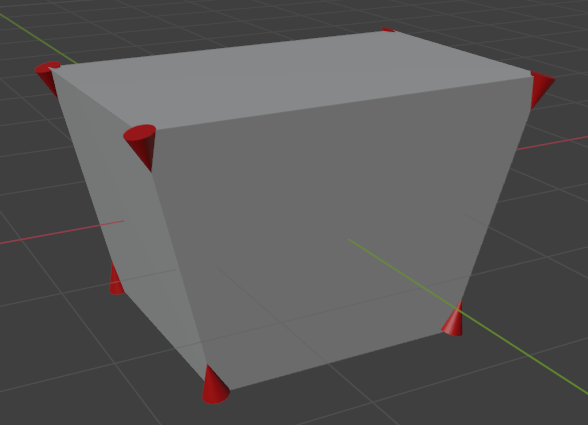
La geometría resultante.¶