Nœud Shortest Edge Paths

Le noeud Shortest Edge Paths trouve des chemins le long des arêtes du maillage vers une sélection de sommets d’extrémité. Le coût utilisé pour définir “le plus court” peut être défini sur n’importe quoi. Par défaut, il y a un coût constant pour chaque arête, mais une entrée typique serait la longueur de chaque arête.

La sortie est codée avec des indices de sommet et est destinée à être utilisée sur le domaine de sommet. Pour chaque sommet, la sortie Next Vertex Input donne l’indice du sommet suivant dans le chemin vers le point de terminaison “le plus proche”.

Le nœud est implémenté avec Dijkstra’s algorithm (l’algorithme de Dijkstra.).

Astuce

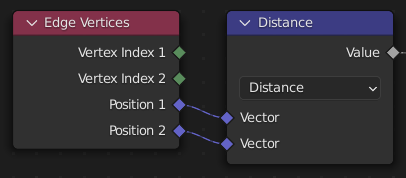
La longueur d’une arête est une donnée naturelle de Edge Cost. Peut être implémenté avec le Nœud Edge Vertices et le Nœud Vector Math réglé sur l’opération Distance.

Voir aussi

Ce nœud peut être utilisé avec le Nœud Paths to Selection ou le Nœud Edge Paths to Curves pour générer une nouvelle géométrie basée sur les chemins.

Inputs

End Vertex

Une sélection des sommets de l’objectif qui terminent le chemin d’arêtes.

Edge Cost

Le poids de chaque arête, utilisé pour déterminer la signification de “shortest” (le plus court.)

Properties

Ce nœud n’a pas de propriétés.

Outputs

Next Vertex Index

Le sommet suivant sur le chemin le plus court entre chaque sommet et l’extrémité la plus proche (tel que défini par le coût d’entrée).

Total Cost

Le coût restant avant qu’un sommet final soit atteint.