Nœud Edges of Vertex

Sélectionne une arête voisine d’un sommet et affiche son index.

Ce nœud est un peu particulier car il opère dans deux domaines différents. Tout d’abord, il évalue un poids (Weight) pour chaque coin de la géométrie. Ensuite, pour chaque élément du domaine contextuel, il sera :

• Choisir un sommet dans la géométrie en fonction de Vertex Index (indice de sommet).

• Trouver les arêtes connectées à ce sommet.

• Trier ces arêtes par leur poids associé.

• Choisisr une arête dans la liste triée ci-dessus en fonction de Sort Index (l’indice de tri), où 0 signifie l’arête avec le poids le plus faible, 1 signifie l’arête avec le deuxième poids le plus bas et ainsi de suite.

• Afficher l’index à l’échelle de la géométrie de cette arête.

Inputs

Vertex Index

L’index du sommet pour lequel trouver les arêtes.

Note

Si cette entrée n’est pas connectée, elle utilise l'index de l’élément de contexte, ce qui signifie qu’il est important que le nœud soit évalué dans le domaine Point.

Weights

Les poids des arêtes dans la géométrie. Contrairement aux autres entrées qui suivent le domaine contextuel, celle-ci est toujours évaluée dans le domaine Edge.

Les arêtes sont triées par leur poids associé par ordre croissant. Les arêtes de même poids sont triées par leur index.

Sort Index

L’index de base 0 de l’arête à sélectionner parmi les arêtes triées du sommet. Si cette valeur est en dehors de la plage des indices valides, elle boucle de l’autre côté.

Properties

Ce nœud n’a pas de propriétés.

Outputs

Edge Index

Index à l’échelle de la géométrie de l’arête sélectionnée. Vous pouvez transmettre cela au Nœud Evaluate at Index ou au Nœud Sample Index (avec le domaine défini sur Edge) pour récupérer des détails sur l’arête.

Si le sommet n’a pas d’arêtes connectées, Edge Index sera nul.

Total

Le nombre d’arêtes connectées au sommet sélectionné.

Exemple

L’exemple ci-dessous crée un cône à chaque sommet d’un “cube”, aligné sur l’arête voisine la plus verticale.

Dans un premier temps, nous calculons un “score de verticalité” pour chacune des arêtes du cube. Pour ce faire, nous soustrayons les positions de ses sommets pour obtenir son vecteur directeur, que nous normalisons et utilisons pour calculer le produit scalaire avec l’axe Z. La valeur absolue de cela nous donne un nombre compris entre 0 et 1, où 0 signifie entièrement horizontal et 1 signifie entièrement vertical.

Étant donné que les arêtes seront triées par poids croissant, nous définissons le poids = 1 - verticalité. De cette façon, l’arête connectée la plus verticale de chaque sommet aura le poids le plus faible et viendra en premier dans la liste.

Ensuite, dans le domaine ponctuel, nous devons calculer la rotation de chaque cône. En utilisant le Nœud Align Rotation to Vector, le problème est simplifié et il suffit de calculer un vecteur directeur.

Le vecteur direction de chaque cône est le centre de l’arête voisine la plus verticale moins la position du sommet. Trouver l’arête voisine la plus verticale est l’endroit où le nœud Edges of Vertex entre en jeu : pour chaque sommet, il trie les arêtes connectées en fonction de leur poids et sélectionne la première (car l’indice de tri est 0). Une fois que nous avons l’index de l’arête, nous utilisons le Nœud Evaluate at Index pour récupérer son point central.

Les rotations des cônes étant calculées, nous utilisons le Nœud Instance on Points pour les créer.

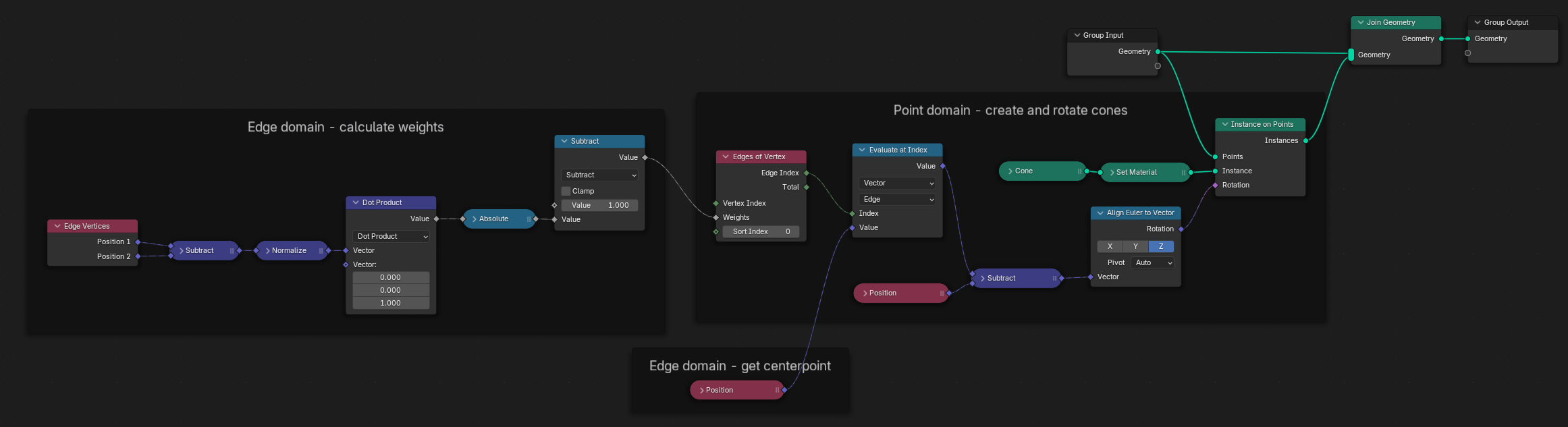
Exemple de configuration de nœud. (Cliquer droit et choisir “Open image in new tab” (Ouvrir l’image dans un nouvel onglet)) pour voir une version plus étendue.)

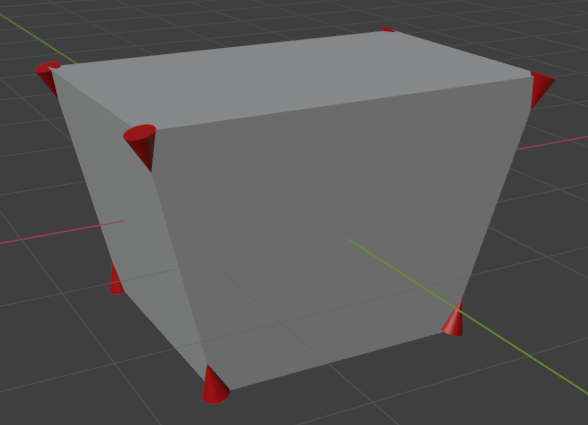
La géométrie résultante.