Introduction – Вступ

Metaball objects (short meta) are implicit surfaces, meaning that they are not explicitly defined by vertices (as meshes are) or control points (as surfaces are): they exist procedurally. Meta objects are literally mathematical formulas that are calculated on-the-fly by Blender.

A very distinct visual characteristic of metas is that they are fluid mercurial, or clay-like forms that have a «rounded» shape. Furthermore, when two meta objects get close to one another, they begin to interact with one another. They «blend» or «merge», as water droplets do, especially in zero-g (which, by the way, makes them very handy for modeling streams of water when you do not want to do a fluid simulation). If they subsequently move away from one another, they restore their original shape.

Кожен з них визначається своєю власною лежачою в основі математичною структурою – structure, і ви можете у будь-який час перемикатися між ними, використовуючи панель «Активний Елемент» – Active Element.

Typically Meta objects are used for special effects or as a basis for modeling. For example, you could use a collection of metas to form the initial shape of your model and then convert it to a mesh for further modeling or sculpting. Meta objects are also very efficient for ray tracing.

Попередження

Names of Meta objects are very important, as they define families, and only objects within a same family interact with each other. Unlike other object types, even editing (transformations) in Object Mode will affect the generated geometry within the edited families.

Visualization – Візуалізація

У Режимі Об’єкта – Object Mode, розрахована сіть показується разом з чорним «кільцем вибрання».

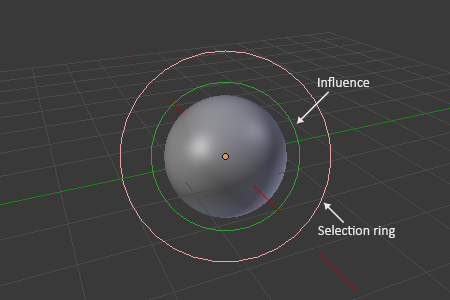
Meta Ball in Edit Mode.

In Edit Mode (Fig. Meta Ball in Edit Mode.), a meta is displayed as a mesh (either shaded or as black wireframe, but without any vertex of course), with two colored circles: a red one for selection (pink when selected), and a green one for a direct control of the meta’s stiffness (light green when active). Note that except for the scale transformation, having the green circle highlighted is equivalent to having the red one.